题目内容
(本题满分12分)
已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 引直线
引直线![]() 交
交![]() 于
于![]() 、
、![]() 两点,
两点,![]() 是坐标原点.
是坐标原点.
(1)求![]()
![]()
![]() 的值;
的值;
(2)若![]() ,且
,且![]() 求直线
求直线![]() 的方程.
的方程.
解(1)由已知得![]() 点坐标为
点坐标为![]()
当![]() 的斜率存在时,设其方程为
的斜率存在时,设其方程为![]()
由![]() ①………2分
①………2分
设![]() ,
,![]() ,则
,则![]()
![]()
![]() ②
②
由①得![]() ,
,![]() 代入②得
代入②得![]()
![]()
![]() ………5分
………5分
当![]() 的斜率不存在时,同样有
的斜率不存在时,同样有![]()
![]()
![]()
综上可知![]()
![]()
![]() ………6分
………6分
(2)由![]() 、
、![]() 、
、![]() 三点共线知
三点共线知![]() ,又
,又![]() ,得
,得![]() ………8分
………8分
当![]() 的斜率不存在时,不符题意;………9分
的斜率不存在时,不符题意;………9分
当![]() 的斜率存在时,由
的斜率存在时,由![]() ,由①及
,由①及![]() 知
知
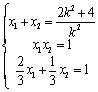 ,消去
,消去![]() ,
,![]() 得
得![]() 或
或![]()
当![]() 时无解;当
时无解;当![]() ,解得
,解得![]() ………11分
………11分
故直线![]() 的方程为
的方程为![]() . ………12分
. ………12分

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面