题目内容
解不等式：
|2x-1|<|x|+1。
|2x-1|<|x|+1。
解：当x＜0时，原不等式可化为-2x+1＜-x+1，解得x>0
又∵x＜0
∴x不存在；
当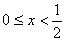
时，原不等式可化为-2x+1＜x+1，解得x>0
又∵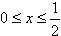
∴
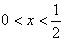
当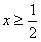
时，原不等式可化为2x-1＜x+1，解得x＜2
又∵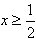
∴
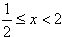
综上，原不等式的解集为{x|0＜x＜2}。
练习册系列答案
相关题目
题目内容
解：当x＜0时，原不等式可化为-2x+1＜-x+1，解得x>0
又∵x＜0
∴x不存在；
当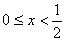时，原不等式可化为-2x+1＜x+1，解得x>0
又∵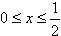
∴
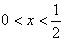
当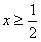时，原不等式可化为2x-1＜x+1，解得x＜2
又∵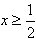
∴
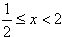
综上，原不等式的解集为{x|0＜x＜2}。