题目内容
如图,等腰直角三角形ABC的斜边AB在x轴上,原点O为AB的中点,|AB|=4,D是OC的中点.以A、B为焦点的椭圆E经过点D.
(1)求椭圆E的方程;
(2)过点C的直线l与椭圆E相交于不同的两点M、N,点M在点C、N之间,且CM=λCN,求实数λ的取值范围.
解:(1)在等腰直角三角形ABC中,因为斜边|AB|=4,
所以|OA|=|OB|=|OC|=2.
所以椭圆的半焦距c=2.
因为D是OC的中点,所以椭圆的短半轴长b=1,
所以椭圆的长半轴长a=![]() .
.
所以椭圆E的方程为![]() +y2=1.
+y2=1.
(2)设M(x1,y1),N(x2,y2),则![]() =(x1,y1-2),
=(x1,y1-2),![]() =(x2,y2-2).
=(x2,y2-2).
由![]() =λ
=λ![]() ,得(x1,y1-2)=λ(x2,y2-2).
,得(x1,y1-2)=λ(x2,y2-2).
所以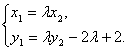 ①
①
因为点M、N都在椭圆![]() +y2=1上,
+y2=1上,
所以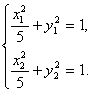 ②
②
将①代入②得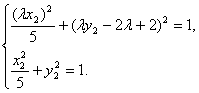
消去x2,得(λy2-2λ+2)2-λ2y22=1-λ2.
所以y2=![]() .
.
根据题意,得-1≤y2≤1,
所以-1≤![]() ≤1.
≤1.
解得![]() ≤λ≤3. ③
≤λ≤3. ③
因为点M在点C、N之间,且![]() =λ
=λ![]() ,
,
所以0<λ<1. ④
根据③④,得![]() ≤λ<1.
≤λ<1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 一个几何体的三视图如图所示,正视图是一个边长为2的正三角形,侧视图是一个等腰直角三角形,则该几何体的体积为
一个几何体的三视图如图所示,正视图是一个边长为2的正三角形,侧视图是一个等腰直角三角形,则该几何体的体积为 如图所示,△ABC是等腰直角三角形,AC=BC=a,P是△ABC所在平面外一点,
如图所示,△ABC是等腰直角三角形,AC=BC=a,P是△ABC所在平面外一点, (2012•通州区一模)已知一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图均为正方形,那么该几何体的表面积是( )
(2012•通州区一模)已知一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图均为正方形,那么该几何体的表面积是( )