Question

【题目】已知函数 .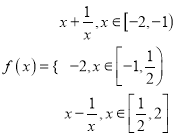

（1）求的值域；

（2）设函数, ，若对于任意, 总存在，使得成立，求实数的取值范围.

Answer 1

【答案】(1) A = [－ ,－2]∪[－ , ];(2) (－,－ ]∪[,+).

【解析】试题分析:（1）先根据各段单调性确定各段值域，最后根据三者值域的并集得函数值域（2）由题意求值域包含值域，再分别求对应值域，最后根据集合包含关系可得实数关系式，解得取值范围.

试题解析: (1) 设，f (x1)－f (x2) = x1 +－(x2 +) = (x1－x2) (1－)

因为，

所以x1－x2 < 0， ， ，所以 1－> 0，

所以 f (x1)－f (x2)< 0， f (x) 在 [－2,－1)是增函数.

同理可证f (x) 在 [,2] 也为增函数（略）

∴ x [－2,－1) 时，f (x) [－,－2)

x [,2] 时，f (x) [－,]

∴ f (x) 的值域 A = [－,－2]∪[－,]

(2) 设 g(x) 的值域为 B，则 B = [－2 | a |－2, 2 | a |－2]

依题意，A B

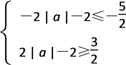
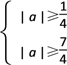| a |≥

∴ a 的取值范围是 (－,－]∪[,+).