题目内容
过点![]() 作已知直线
作已知直线![]() 的平行线,交双曲线
的平行线,交双曲线![]() 于点
于点![]() .
.
(1)证明:点![]() 是线段
是线段![]() 的中点.
的中点.
(2)分别过点![]() 作双曲线的切线
作双曲线的切线![]() ,证明:三条直线
,证明:三条直线![]() 相交于同一点.
相交于同一点.
(3)设![]() 为直线
为直线![]() 上一动点,过点
上一动点,过点![]() 作双曲线的切线
作双曲线的切线![]() ,切点分别为
,切点分别为![]() .证明:点
.证明:点![]() 在直线AB上.
在直线AB上.
证明略
解析:
(1)直线![]() 的方程为
的方程为![]() ,即
,即![]() ,代入双曲线方程
,代入双曲线方程![]() ,得
,得 ![]() .
.
设![]() ,则
,则![]() 是方程的两根,所以
是方程的两根,所以![]() ,
,
于是![]() ,故点
,故点![]() 是线段
是线段![]() 的中点. ………5分
的中点. ………5分
(2)双曲线![]() 的过点
的过点![]() 的切线方程分别为
的切线方程分别为
![]() ,
,![]() .
.
联立,得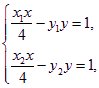 两式相加,并将
两式相加,并将![]() ,
,![]() 代入,得
代入,得![]() ,这说明直线
,这说明直线![]() 的交点在直线
的交点在直线![]() 上,即三条直线
上,即三条直线![]() 相交于同一点. …………………………10分
相交于同一点. …………………………10分
(3)设![]() ,
,![]() ,则
,则![]() 的方程分别为
的方程分别为![]() 和
和![]() ,因为点
,因为点![]() 在两条直线上,所以
在两条直线上,所以![]() ,
,![]() ,这表明点
,这表明点![]() 都在直线
都在直线![]() 上,即直线
上,即直线![]() 的方程为
的方程为![]() .
.
又![]() ,代入整理得
,代入整理得![]() ,显然,无论
,显然,无论![]() 取什么值(即无论
取什么值(即无论![]() 为直线
为直线![]() 上哪一点),点
上哪一点),点![]() 都在直线AB上. …………………………20分
都在直线AB上. …………………………20分

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 (2011•潍坊二模)如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是4
(2011•潍坊二模)如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是4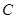 过点
过点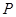
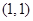 ,且与圆
,且与圆
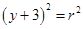 (
(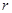 >0)关于直线
>0)关于直线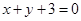 对称,
对称,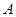 、
、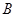 ,且直线
,且直线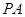 和直线
和直线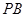 的倾斜角互补,
的倾斜角互补,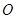 为坐标原点,判断直线
为坐标原点,判断直线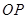 与
与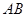 是否平行,并请说明理由
是否平行,并请说明理由