题目内容
(本题满分16分)已知圆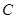 过点
过点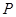
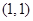 ,且与圆
,且与圆
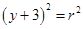 (
(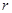 >0)关于直线
>0)关于直线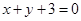 对称,
对称,
⑴求圆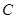 的方程;
的方程;
⑵过点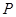 作两条直线分别与圆
作两条直线分别与圆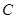 相交于点
相交于点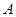 、
、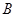 ,且直线
,且直线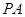 和直线
和直线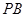 的倾斜角互补,
的倾斜角互补,
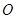 为坐标原点,判断直线
为坐标原点,判断直线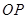 与
与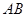 是否平行,并请说明理由
是否平行,并请说明理由
【答案】
解:(1)依题意,可设圆 的方程为
的方程为
 ,且
,且 、
、 满足方程组
满足方程组

由此解得

又因为点
 在圆
在圆 上,所以
上,所以
 .
.
故圆 的方程为
的方程为 .
.
(2)由题意可知,直线 和直线
和直线 的斜率存在且互为相反数
的斜率存在且互为相反数
故可设 所在的直线方程为
所在的直线方程为 ,
, 所在的直线方程为
所在的直线方程为 .
.
由 消去
消去 ,并整理得
,并整理得  .①
.①
设 ,又已知P
,又已知P ,则
,则 、1为方程①的两相异实数根,由根与系数的关系得
、1为方程①的两相异实数根,由根与系数的关系得
同理,若设点B  ,则可得
,则可得 .
.
于是 =
= =1.
=1.
而直线 的斜率也是1,且两直线不重合,因此,直线
的斜率也是1,且两直线不重合,因此,直线 与
与 平行
平行
【解析】略

练习册系列答案
相关题目
 ,且对任意
,且对任意 ,有
,有 .
. ;
; 在区间(0,1)上为单调函数,求实
在区间(0,1)上为单调函数,求实 数
数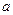 的取值范围.
的取值范围. 的零点个数?(提示
的零点个数?(提示 )
) 为实常数).
为实常数). 时,求函数
时,求函数 在
在 上的最小值;
上的最小值; 在区间
在区间 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
 )
) :
: 的离心率为
的离心率为 ,
, 分别为椭圆
分别为椭圆 为椭圆上任意一点,以
为椭圆上任意一点,以 为半径作圆
为半径作圆 有公共点时,求△
有公共点时,求△ 面积的最大值.
面积的最大值. 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时, 。
。 及
及 的值;
的值; 上的解析式;
上的解析式; 的方程
的方程 有四个不同的实数解,求实数
有四个不同的实数解,求实数 的取值范围。
的取值范围。