题目内容
（2012•虹口区三模）已知数列{an}中，a1=1，a2=3，对任意n∈N*，an+2≤an+3•2n，an+1≥2an+1都成立，则a11-a10=
1024
1024
．分析：由an+2≤an+3•2n，an+1≥2an+1都成立，且a1=1，a2=3，可分别求解a3≤a1+6=7a3≥2a2+1=7，a4≤a2+12=15，a4≥2a3+1=15，从而可求数列的项
解答：解：∵an+2≤an+3•2n，an+1≥2an+1都成立，且a1=1，a2=3，
∴a3≤a1+6=7，a3≥2a2+1=7
∴a3=7
a4≤a2+12=15，a4≥2a3+1=15
∴a4=15
以此类推，a5=31，a6=63，a7=27-1，…a10=210-1，a11=211-1
∴a11-a10=211-210=210=1024
故答案为：1024
∴a3≤a1+6=7，a3≥2a2+1=7
∴a3=7
a4≤a2+12=15，a4≥2a3+1=15
∴a4=15
以此类推，a5=31，a6=63，a7=27-1，…a10=210-1，a11=211-1
∴a11-a10=211-210=210=1024
故答案为：1024
点评：本题主要考查了利用数列的递推公式求解数列的项，解题的关键是由不等关系得到等式
练习册系列答案
相关题目
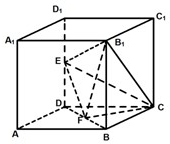（2012•虹口区三模）如图所示，在棱长为2的正方体ABCD-A1B1C1D1中，E、F分别为DD1、DB的中点．
（2012•虹口区三模）函数y=2x和y=x3的图象的示意图如图所示，设两函数的图象交于点A（x1，y1），B（x2，y2），且x1＜x2．