题目内容
设不等式组 表示的平面区域为D,若指数函数y=ax的图象上存在区域D上的点,则a的取值范围是
表示的平面区域为D,若指数函数y=ax的图象上存在区域D上的点,则a的取值范围是
- A.(1,3]
- B.(2,3]
- C.(2,+∞)
- D.[3,+∞)
B
分析:先依据不等式组 ,结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用指数函数y=ax的图象特征,结合区域的角上的点即可解决问题.
,结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用指数函数y=ax的图象特征,结合区域的角上的点即可解决问题.
解答: 解:作出区域D的图象,联系指数函数y=ax的图象,能够看出,
解:作出区域D的图象,联系指数函数y=ax的图象,能够看出,
只要a大于1,图象才可能经过区域内的点.
当图象经过区域的边界点A(2,4)时,a可以取到最小值2,但区域不包括A点;
图象经过区域的边界点B(1,3)时,a可以取到最大值3,
则a的取值范围是(2,3]
故选B.
点评:这是一道略微灵活的线性规划问题,本题主要考查了用平面区域二元一次不等式组、指数函数的图象与性质,以及简单的转化思想和数形结合的思想,属中档题.
分析:先依据不等式组
 ,结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用指数函数y=ax的图象特征,结合区域的角上的点即可解决问题.
,结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用指数函数y=ax的图象特征,结合区域的角上的点即可解决问题.解答:
 解:作出区域D的图象,联系指数函数y=ax的图象,能够看出,
解:作出区域D的图象,联系指数函数y=ax的图象,能够看出,只要a大于1,图象才可能经过区域内的点.
当图象经过区域的边界点A(2,4)时,a可以取到最小值2,但区域不包括A点;
图象经过区域的边界点B(1,3)时,a可以取到最大值3,
则a的取值范围是(2,3]
故选B.
点评:这是一道略微灵活的线性规划问题,本题主要考查了用平面区域二元一次不等式组、指数函数的图象与性质,以及简单的转化思想和数形结合的思想,属中档题.

练习册系列答案
相关题目
 表示的平面区域为D,若指数函数y=
表示的平面区域为D,若指数函数y= 的图像上存在区域D上的点,则a 的取值范围是 ( )
的图像上存在区域D上的点,则a 的取值范围是 ( ) B.
B. C.
C. D.
D.
 表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是( )
表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是( )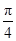 B.
B.  C.
C.  D.
D. 
 表示的平面区域的面积为
表示的平面区域的面积为 ,若
,若 ,则
,则 满足
满足 B.
B.
 D.
D.
 表示的平面区域为D,若指数函数y=
表示的平面区域为D,若指数函数y= 的图像上存在区域D上的点,则a 的取值范围是
( )
的图像上存在区域D上的点,则a 的取值范围是
( ) B.
B.
 C.
C. D.
D. 
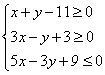 表示的平面区域为D,若指数函数y=
表示的平面区域为D,若指数函数y= 的图像上
的图像上 ]
]