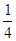题目内容
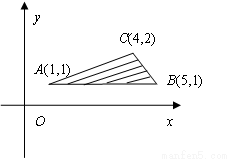
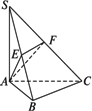
如下图所示,SA⊥平面ABC,AB⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F.求证:AF⊥SC.
证明:要证AF⊥SC,只需证SC⊥平面AEF,只需证AE⊥SC(因为___________),只需证___________,只需证AE⊥BC(因为___________),只需证BC⊥平面SAB,只需证BC⊥SA(因为___________).由SA⊥平面ABC可知,上式成立.所以,AF⊥SC.
思路分析:要证线线垂直,可先证线面垂直;要证线面垂直.还需线线垂直,通过证明BC⊥平面SAB,可得AE⊥BC;进而AE⊥平面SBC,SC⊥平面AEF,问题得证.
答案:EF⊥SC AE⊥平面SBC AE⊥SB AB⊥BC

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
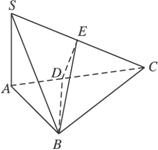

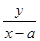 的最大值是 ( )
的最大值是 ( )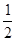 C.
C.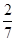 D.
D.