题目内容
如图,已知AB=2c(常数c>0),以AB为直径的圆有一内接梯形ABCD,且AB∥CD,若椭圆以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,椭圆的离心率为______.
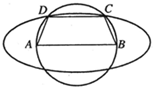

设∠BAC=θ,过C作CE⊥AB,垂足为E,则
BC=2csinθ,EB=BCcos(90°-θ)=2csin2θ,∴CD=2c-4csin2θ,
梯形的周长l=AB+2BC+CD=2c+4csinθ+2c-4csin2=-4c(sinθ-
)2+5c.
当sinθ=
,即θ=30°时,l有最大值5c,这时,BC=c,AC=
c,a=
(AC+BC)=
c,
∴e=
=
=
-1.
故答案
-1

BC=2csinθ,EB=BCcos(90°-θ)=2csin2θ,∴CD=2c-4csin2θ,
梯形的周长l=AB+2BC+CD=2c+4csinθ+2c-4csin2=-4c(sinθ-
| 1 |
| 2 |
当sinθ=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∴e=
| c |
| a |
| c | ||||
|
| 3 |
故答案
| 3 |


练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目