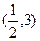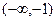题目内容
已知函数 a、c∈R满足条件:①f(1)=0;②对一切x∈R,都有f(x)≥0.
a、c∈R满足条件:①f(1)=0;②对一切x∈R,都有f(x)≥0.(Ⅰ)求a、c的值;
(Ⅱ)是否存在实数m,使函数g(x)=f(x)-mx在区间[m,m+2]上有最小值-5?若存在,请求出实数m的值;若不存在,请说明理由.
【答案】分析:(Ⅰ)首先函数 是二次函数,再利用二次函数的性质解决对一切x∈R,都有f(x)≥0;根据f(1)=0得
是二次函数,再利用二次函数的性质解决对一切x∈R,都有f(x)≥0;根据f(1)=0得  ,即
,即 ,从而可得
,从而可得  ,进而可得
,进而可得 ,
, ,
,
另解:首先函数 是二次函数,再利用二次函数的性质解决对一切x∈R,都有f(x)≥0;由f(1)=0,得
是二次函数,再利用二次函数的性质解决对一切x∈R,都有f(x)≥0;由f(1)=0,得  ,代入上式得
,代入上式得  ,根据
,根据  ,可得
,可得 ,从而有
,从而有  ,故可求a、c的值;
,故可求a、c的值;
(Ⅱ) .该函数图象开口向上,且对称轴为x=2m+1.假设存在实数m使函数
.该函数图象开口向上,且对称轴为x=2m+1.假设存在实数m使函数 在区间[m,m+2]上有最小值-5.根据函数的对称轴与区间的关系进行分类讨论,从而可求m的值
在区间[m,m+2]上有最小值-5.根据函数的对称轴与区间的关系进行分类讨论,从而可求m的值
解答:解:(Ⅰ)当a=0时, .
.
由f(1)=0得: ,即
,即 ,∴
,∴ .
.
显然x>1时,f(x)<0,这与条件②相矛盾,不合题意.
∴a≠0,函数 是二次函数. …(2分)
是二次函数. …(2分)
由于对一切x∈R,都有f(x)≥0,于是由二次函数的性质可得

即 (*)…(4分)
(*)…(4分)
由f(1)=0得 ,即
,即 ,代入(*)得
,代入(*)得  .
.
整理得 ,即
,即 .
.
而 ,∴
,∴ .
.
将 代入(*)得,
代入(*)得, ,
,
∴ . …(7分)
. …(7分)
另解:(Ⅰ)当a=0时, .
.
由f(1)=0得 ,即
,即 ,
,
∴ .
.
显然x>1时,f(x)<0,这与条件②相矛盾,
∴a≠0,因而函数 是二次函数. …(2分)
是二次函数. …(2分)
由于对一切x∈R,都有f(x)≥0,于是由二次函数的性质可得

即 …(4分)
…(4分)
由此可知 a>0,c>0,
∴ .
.
由f(1)=0,得 ,代入上式得
,代入上式得  .
.
但前面已推得 ,
,
∴ .
.
由 解得
解得  . …(7分)
. …(7分)
(Ⅱ)∵ ,∴
,∴ .
.
∴ .
.
该函数图象开口向上,且对称轴为x=2m+1. …(8分)
假设存在实数m使函数 在区间[m,m+2]上有最小值-5.
在区间[m,m+2]上有最小值-5.
①当m<-1时,2m+1<m,函数g(x)在区间[m,m+2]上是递增的,
∴g(m)=-5,
即 ,
,
解得 m=-3或m= .
.
∵ >-1,∴m=
>-1,∴m= 舍去. …(10分)
舍去. …(10分)
②当-1≤m<1时,m≤2m+1<m+1,函数g(x)在区间[m,2m+1]上是递减的,而在区间[2m+1,m+2]上是递增的,
∴g(2m+1)=-5,
即 .
.
解得 m= 或m=
或m= ,均应舍去. …(12分)
,均应舍去. …(12分)
③当m≥1时,2m+1≥m+2,函数g(x)在区间[m,m+2]上是递减的,
∴g(m+2)=-5,
即 .
.
解得 m= 或m=
或m= ,其中m=
,其中m= 应舍去.
应舍去.
综上可得,当m=-3或m= 时,函数g(x)=f(x)-mx在区间[m,m+2]上有最小值-5.
时,函数g(x)=f(x)-mx在区间[m,m+2]上有最小值-5.
…(14分)
点评:本小题主要考查函数、方程、不等式等基本知识,考查综合运用数学知识分析和解决问题的能力,本题考查的重点是函数的解析式的求解与函数最值的研究,解题的关键是合理运用函数的性质,正确分类,同时考查学生分析解决问题的能力,有一定的综合性.
 是二次函数,再利用二次函数的性质解决对一切x∈R,都有f(x)≥0;根据f(1)=0得
是二次函数,再利用二次函数的性质解决对一切x∈R,都有f(x)≥0;根据f(1)=0得  ,即
,即 ,从而可得
,从而可得  ,进而可得
,进而可得 ,
, ,
,另解:首先函数
 是二次函数,再利用二次函数的性质解决对一切x∈R,都有f(x)≥0;由f(1)=0,得
是二次函数,再利用二次函数的性质解决对一切x∈R,都有f(x)≥0;由f(1)=0,得  ,代入上式得
,代入上式得  ,根据
,根据  ,可得
,可得 ,从而有
,从而有  ,故可求a、c的值;
,故可求a、c的值;(Ⅱ)
 .该函数图象开口向上,且对称轴为x=2m+1.假设存在实数m使函数
.该函数图象开口向上,且对称轴为x=2m+1.假设存在实数m使函数 在区间[m,m+2]上有最小值-5.根据函数的对称轴与区间的关系进行分类讨论,从而可求m的值
在区间[m,m+2]上有最小值-5.根据函数的对称轴与区间的关系进行分类讨论,从而可求m的值解答:解:(Ⅰ)当a=0时,
 .
.由f(1)=0得:
 ,即
,即 ,∴
,∴ .
.显然x>1时,f(x)<0,这与条件②相矛盾,不合题意.
∴a≠0,函数
 是二次函数. …(2分)
是二次函数. …(2分)由于对一切x∈R,都有f(x)≥0,于是由二次函数的性质可得

即
 (*)…(4分)
(*)…(4分)由f(1)=0得
 ,即
,即 ,代入(*)得
,代入(*)得  .
.整理得
 ,即
,即 .
.而
 ,∴
,∴ .
.将
 代入(*)得,
代入(*)得, ,
,∴
 . …(7分)
. …(7分)另解:(Ⅰ)当a=0时,
 .
.由f(1)=0得
 ,即
,即 ,
,∴
 .
.显然x>1时,f(x)<0,这与条件②相矛盾,
∴a≠0,因而函数
 是二次函数. …(2分)
是二次函数. …(2分)由于对一切x∈R,都有f(x)≥0,于是由二次函数的性质可得

即
 …(4分)
…(4分)由此可知 a>0,c>0,
∴
 .
.由f(1)=0,得
 ,代入上式得
,代入上式得  .
.但前面已推得
 ,
,∴
 .
.由
 解得
解得  . …(7分)
. …(7分)(Ⅱ)∵
 ,∴
,∴ .
.∴
 .
.该函数图象开口向上,且对称轴为x=2m+1. …(8分)
假设存在实数m使函数
 在区间[m,m+2]上有最小值-5.
在区间[m,m+2]上有最小值-5.①当m<-1时,2m+1<m,函数g(x)在区间[m,m+2]上是递增的,
∴g(m)=-5,
即
 ,
,解得 m=-3或m=
 .
.∵
 >-1,∴m=
>-1,∴m= 舍去. …(10分)
舍去. …(10分)②当-1≤m<1时,m≤2m+1<m+1,函数g(x)在区间[m,2m+1]上是递减的,而在区间[2m+1,m+2]上是递增的,
∴g(2m+1)=-5,
即
 .
.解得 m=
 或m=
或m= ,均应舍去. …(12分)
,均应舍去. …(12分)③当m≥1时,2m+1≥m+2,函数g(x)在区间[m,m+2]上是递减的,
∴g(m+2)=-5,
即
 .
.解得 m=
 或m=
或m= ,其中m=
,其中m= 应舍去.
应舍去.综上可得,当m=-3或m=
 时,函数g(x)=f(x)-mx在区间[m,m+2]上有最小值-5.
时,函数g(x)=f(x)-mx在区间[m,m+2]上有最小值-5.…(14分)
点评:本小题主要考查函数、方程、不等式等基本知识,考查综合运用数学知识分析和解决问题的能力,本题考查的重点是函数的解析式的求解与函数最值的研究,解题的关键是合理运用函数的性质,正确分类,同时考查学生分析解决问题的能力,有一定的综合性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)为R上的连续函数且存在反函数f-1(x),若函数f(x)满足下表:

那么,不等式|f-1(x-1)|<2的解集是( )

那么,不等式|f-1(x-1)|<2的解集是( )
A、{x|
| ||
B、{x|
| ||
| C、{x|1<x<2} | ||
| D、{x|1<x<5} |

 <x<4}
<x<4} <x<3}
<x<3}
 <x<4}
<x<4} <x<3}
<x<3} 是定义域为R的奇函数,
是定义域为R的奇函数, ,
, 的图象如图所示.若两正数
的图象如图所示.若两正数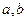 满 足
满 足 ,则
,则 的取值范围是( )
的取值范围是( )