题目内容
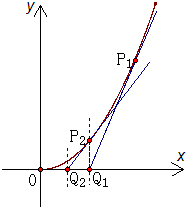
如图，曲线段C是函数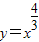
（x≥0）的图象，C过点P1（1，1）．过P1作曲线C的切线交x轴于Q1点，过Q1作垂直于x轴的直线交曲线C于P2点，过P2的切线交x轴于Q2点，…，如此反复，得到一系列点Q1，Q2，…，Qn，设Qn（an，0）．（1）求a1；
（2）求an的表达式；
（3）证明：
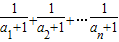
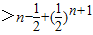（n∈N*）．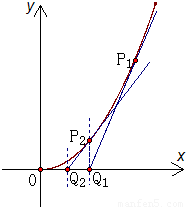
【答案】分析：（1）求导函数，求得过P1切线方程，即可求得a1；
（2）确定过
的切线方程，利用直线过Qn+1（an+1，0），可得an的表达式；
（3）证明
，累加即可证得结论．
解答：（1）解：
，则
…（2分）
过P1切线方程：
，可得
，则
． …（4分）
（2）解：
，过
的切线方程：
，…（6分）
该直线过Qn+1（an+1，0），则
化简得
，则
…（8分）
（3）证明：
，…（9分）
而4n+1＞2•2n=2n+1，故
…（11分）
所以
=
=
所以
…（14分）
点评：本题考查数列与函数的综合，考查数列的通项，考查不等式的证明，确定数列的通项是关键．
（2）确定过
的切线方程，利用直线过Qn+1（an+1，0），可得an的表达式；（3）证明
，累加即可证得结论．解答：（1）解：
，则…（2分）过P1切线方程：
，可得，则． …（4分）（2）解：
，过的切线方程：，…（6分）该直线过Qn+1（an+1，0），则
化简得
，则…（8分）（3）证明：
，…（9分）而4n+1＞2•2n=2n+1，故
…（11分）所以
==所以
…（14分）点评：本题考查数列与函数的综合，考查数列的通项，考查不等式的证明，确定数列的通项是关键．
练习册系列答案
相关题目
如图，曲线段C是函数