题目内容
曲线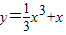
在点
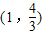处的切线与坐标轴围成的三角形面积为（ ）A．
B．
C．
D．
【答案】分析：（1）首先利用导数的几何意义，求出曲线在P（x，y）处的切线斜率，进而得到切线方程；（2）利用切线方程与坐标轴直线方程求出交点坐标（3）利用面积公式求出面积．
解答：解：若y=
x3+x，则y′|x=1=2，即曲线
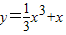在点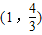
处的切线方程是
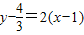，它与坐标轴的交点是（
，0），（0，-
），围成的三角形面积为
，故选A．
点评：函数y=f（x）在x=x处的导数的几何意义，就是曲线y=f（x）在点P（x，y）处的切线的斜率，过点P的切线方程为：y-y=f′（x）（x-x）
解答：解：若y=
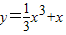x3+x，则y′|x=1=2，即曲线在点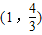处的切线方程是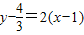，它与坐标轴的交点是（，0），（0，-），围成的三角形面积为，故选A．点评：函数y=f（x）在x=x处的导数的几何意义，就是曲线y=f（x）在点P（x，y）处的切线的斜率，过点P的切线方程为：y-y=f′（x）（x-x）
练习册系列答案
名校课堂系列答案
相关题目
在点
处的切线与坐标轴所围三角形的面积为 。
在点
处的切线与坐标轴所围三角形的面积为（ ）
B．
C．
D．
在点
处的切线与坐标轴所围成的三角形的面积为（ ）
B．
C．
D．
在点
处的切线与坐标轴所围三角形的面积为
.
在点
处的切线与坐标轴围成的三角形面积为（ ）
B．
C．
D．