题目内容

1．若在1和2之间插人n个正数，使这n+2个数成等比数列，则插人的这n个数的积等于${2}^{\frac{n}{2}}$．

分析 由等比数列的性质可得a1an=1•2=2，a2an-1=2，…，从而解得．

解答 解：设n个正数为a1，a2，a3，…，an-1，an；
∵1，a1，a2，a3，…，an-1，an，2成等比数列，
∴a1an=1•2=2，a2an-1=2，…，
∴a1a2a3…an-1an=${2}^{\frac{n}{2}}$，
故答案为：${2}^{\frac{n}{2}}$．

点评 本题考查了等比数列的性质的应用．

练习册系列答案
相关题目
11．已知函数f（x）=$\left\{\begin{array}{l}{（a-\frac{1}{3}）x+3，x≤0}\\{{a}^{x}，x＞0}\end{array}\right.$在区间（-∞，+∞）内是减函数，则a的取值范围是（$\frac{1}{3}$，1）．
12．已知函数f（x）=${log}_{\frac{1}{2}}$（$\frac{1}{2}$sin2x）．
（1）求f（x）的定义域、值域和单调区间
（2）判断f（x）的奇偶性．
9．已知函数f（x）=2sin（2x+φ）（|φ|＜$\frac{π}{2}$）在区间（-$\frac{π}{12}$，$\frac{π}{6}$]上单调且最大值不大于$\sqrt{3}$，则φ的取值范围是（　　）
A．[0，$\frac{π}{3}$]B．[$-\frac{π}{3}$，$\frac{π}{6}$]C．（$-\frac{π}{4}$，0]D．[$-\frac{π}{3}$，0]
16．设α，β，γ∈（0，$\frac{π}{2}$），且sinα+sinγ=sinβ，cosα-cosγ=cosβ，则α-β的值为（　　）
A．-$\frac{π}{3}$B．$\frac{π}{6}$C．$\frac{π}{3}$或-$\frac{π}{3}$D．$\frac{π}{3}$
6．已知{an}是等差数列，Sn为其前n项和，若正整数i，j，k，l满足i≤k≤l≤j，且i+j=k+l，则（　　）
A．aiaj≤akalB．aiaj≥akalC．SiSj＜SkSlD．SiSj≥SkSl
13．已知A、B、C为△ABC的三个内角，向量$\overrightarrow{m}$满足|$\overrightarrow{m}$|=$\frac{\sqrt{6}}{2}$，且$\overrightarrow{m}$=（$\sqrt{2}$sin$\frac{B+C}{2}$，cos$\frac{B-C}{2}$），若A最大时，动点P使得|$\overrightarrow{PB}$|、|$\overrightarrow{BC}$|、|$\overrightarrow{PC}$|成等差数列，则$\frac{|\overrightarrow{PA}|}{|\overrightarrow{BC}|}$的最大值是（　　）
A．$\frac{2\sqrt{3}}{3}$B．$\frac{2\sqrt{2}}{3}$C．$\frac{\sqrt{2}}{4}$D．$\frac{3\sqrt{2}}{4}$
12．设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的一个焦点为F，虚轴的一个端点为B，线段BF与双曲线的一条渐近线交于点A，若$\overrightarrow{FA}=2\overrightarrow{AB}$，则双曲线的离心率为2．
13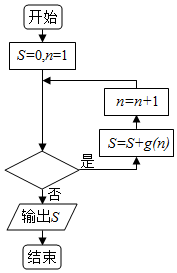．已知函数f（x）=ax3+$\frac{1}{2}$x2在x=-1处取得极大值，记g（x）=$\frac{1}{f′（x）}$．在如图所示的程序框图中，若输出的结果S=$\frac{2016}{2017}$，则判断框中可以填入的关于n的判断条件是（　　）
A．n≤2016？B．n≤2017？C．n＞2016？D．n＞2017？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网