题目内容
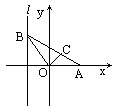
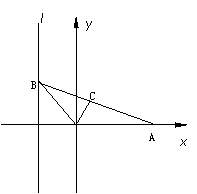
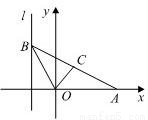
如图,给出定点A(a,0)(a>0)和直线l:x=-1,B是直线l上的动点,∠BOA的平分线交AB于C点,求点C的轨迹方程.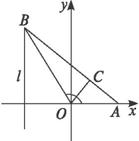
思路解析:根据角的平分线这一条件,可以考虑点到两边的距离;也可以考虑角的关系;还可以考虑角的平分线定理.
解法一:由题意,设B(-1,t)(t为参数),则直线OB的方程为y=-tx;设点C(x,y),则有0≤x<a.由OC平分∠AOB知,∠AOB平分线上的点C到OA、OB距离相等.
∴|y|=![]() . ①
. ①
又∵AB的斜率为![]() =-
=-![]() ,
,
∴直线AB的方程为y=-![]() (x-a).
(x-a).
由于x-a≠0,
∴t=-![]() y. ②
y. ②
将②代入①并化简,得y2[1+y2(![]() )2]=[y-
)2]=[y-![]() ]2.
]2.
整理,得y2[(1-a)x2-2ax+(1+a)y2]=0.
当y≠0时,(1-a)x2-2ax+(1+a)y2=0(0<x<a);
当y=0时,由②知t=0,∠AOB=180°,C(0,0)仍满足上式,此时x=0.
综上得,C点的轨迹方程为(1-a)x2-2ax+(1+a)y2=0(0≤x<a![]() .
.
解法二:设C(x,y)(0≤x<a=并设OC的斜率为k,则直线OC的方程为y=kx. ①
由OC平分∠AOB,∴OB的斜率为![]() .∴直线OB的方程为y=
.∴直线OB的方程为y=![]() x.
x.
令x=-1,得点B(-1,-![]() ).又点A(a,0),
).又点A(a,0),
∴AB的斜率为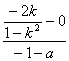 =
=![]() .
.
∴直线AB的方程为y=![]() (x-a). ②
(x-a). ②
当点C不在原点,即x>0时,①化为k=![]() ,代入②得
,代入②得
y2[(1-a)x2-2ax+(1+a)y2]=0.(以下同解法一,略去).
解法三:设点C(x,y),则0≤x<a.当x≠0时,kOC=![]() .由OC平分∠AOB,
.由OC平分∠AOB,
∴∠AOB=2∠AOC.∴kOB=![]() =
=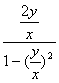 =
=![]() .
.
另一方面,点B横坐标为-1,
∴![]() =kOB.∴yB=
=kOB.∴yB=![]() ,即B(-1,
,即B(-1,![]() ).
).
由三点A、C、B共线且A(a,0),∴![]() =
=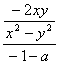 .
.
化简,得(1-a)x2-2ax+(1+a)y2=0.
当x=0时,由题意得点C为原点,即C(0,0)仍满足上面方程.
∴动点C的轨迹方程为(1-a)x2-2ax+(1+a)y2=0(0≤x<a).
解法四:设C(x,y)及点B(-1,t)(t为参数).∵OC平分∠AOB,由三角形内角平分线定理得![]() =
=![]() .而
.而![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() .由
.由![]() =
=![]() 解得
解得
t=![]() .代入
.代入![]() =
=![]() ,
,
化简,得(1-a)x2-2ax+(1+a)y2=0(0≤x<a),此式即为所求动点C的轨迹方程?.

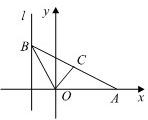 如图,给出定点A(a,0)(a>0,a≠1)和直线l:x=-1,B是直线l上的动点,∠BOA的角平分线交AB于点C.求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.
如图,给出定点A(a,0)(a>0,a≠1)和直线l:x=-1,B是直线l上的动点,∠BOA的角平分线交AB于点C.求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.