题目内容
如图，已知三点A，B，E在平面
内，点C，D在外，并且
，
。若AB=3，AC=BD=4，CD=5，则BD与平面所成的角等于（ ）
内，点C，D在外，并且，。若AB=3，AC=BD=4，CD=5，则BD与平面所成的角等于（ ）A． | B． |
C． | D． |
C
∵DE⊥α，
∴BE即为BD在平面α内的射影，
可得∠DBE是直线BD与平面α所成的角
过点D作DF⊥AC于F，连接AD，AE
∵AC⊥α，DE⊥α，
∴AC∥DE，且∠AED=∠FAE=∠DFA=90°
可得四边形AEDF为矩形
∴DE=AF
∵BD⊥AB
∴Rt△ABD中，AD=
=
=5
∵△ACD中，CD=AD=5
∴DF是中线，即AF=CF=
AC=2
∴Rt△BDE中，BD=4，DE=2
可得sin∠DBE=
=
∴∠DBE=30°，即直线BD与平面α所成的角等于30°
故选C
∴BE即为BD在平面α内的射影，
可得∠DBE是直线BD与平面α所成的角
过点D作DF⊥AC于F，连接AD，AE
∵AC⊥α，DE⊥α，
∴AC∥DE，且∠AED=∠FAE=∠DFA=90°
可得四边形AEDF为矩形
∴DE=AF
∵BD⊥AB
∴Rt△ABD中，AD=
==5∵△ACD中，CD=AD=5
∴DF是中线，即AF=CF=
AC=2∴Rt△BDE中，BD=4，DE=2
可得sin∠DBE=
=∴∠DBE=30°，即直线BD与平面α所成的角等于30°
故选C
练习册系列答案
阅读快车系列答案
相关题目
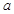，则相邻两个面的夹角的余弦是 
BB1，则AB1与C1B所成角的大小为
，
=
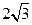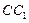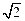，二面角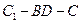
的大小为 ▲ ．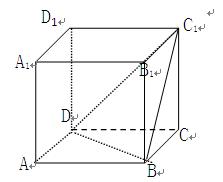
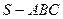中，底面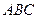
为边长等于2的等边三角形，
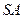垂直于底面
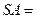
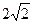，D为
，AD=1，在DC上截取DE=1，将△ADE沿AE
求角A