题目内容
【题目】给定函数
和
，若存在常数
，
，使得函数和对其公共定义域
的任何实数
分别满足
和
，则称直线
：
为函数和的“隔离直线”，给出下列四组函数：
（1）
，
； （2）
，
；
（3）
，
； （4）
，
；
其中函数和存在“隔离直线”的序号是（ ）
A.（1）（3）B.（1）（3）（4）C.（1）（2）（3）D.（2）（4）
【答案】A
【解析】
逐一分析每组函数图象，并画出函数图象，从函数的定义域，值域和图象共同分析是否有满足条件的直线.
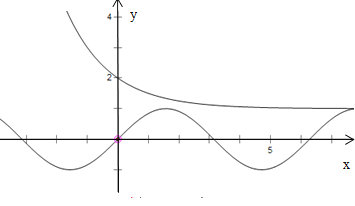
A.如图画出函数的图象，两个函数的公共定义域是
，
的值域是
，
的值域是
，所以存在直线
满足条件，此时
，故成立；
B.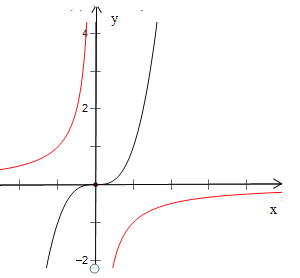 
两个函数的公共定义域是
，由图象可知当
时，
，当
时，
，没有直线
满足条件，故不成立；
C.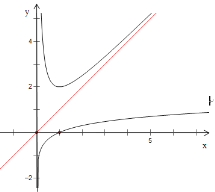 
函数
和
公共定义域是
，图象如图所示，很明显存在直线满足条件，例：当
时满足条件，故正确；
D.函数的公共定义域是
，
和
都是增函数，画出函数的图象，
图象有两个交点，显然不存在直线满足条件，故不成立.
正确的有（1）（3）
故选：A
练习册系列答案
相关题目
