题目内容
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的50位顾客的相关数据,如下表所示:
已知这50位顾客中一次购物量少于10件的顾客占80%.
(1)确定x与y的值;
(2)若将频率视为概率,求顾客一次购物的结算时间X的分布列与数学期望;
(3)在(2)的条件下,若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2分钟的概率.
| 一次购物量n(件) | 1≤n≤3 | 4≤n≤6 | 7≤n≤9 | 10≤n≤12 | n≥13 |
| 顾客数(人) | x | 20 | 10 | 5 | y |
| 结算时间(分钟/人) | 0.5 | 1 | 1.5 | 2 | 2.5 |
(1)确定x与y的值;
(2)若将频率视为概率,求顾客一次购物的结算时间X的分布列与数学期望;
(3)在(2)的条件下,若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2分钟的概率.
分析:(1)由表格中的数据计算出,x,y的值.
(2)求出随机变量的分布列,利用分布列求出数学期望.
(3)根据独立事件同时发生的公式,求概率.
(2)求出随机变量的分布列,利用分布列求出数学期望.
(3)根据独立事件同时发生的公式,求概率.
解答:(1)依题意得,x+20+10=50×80%,5+y=50×20%,解得x=10,y=5.
(2)该超市所有顾客一次购物的结算时间组成一个总体,所以收集的50位顾客一次购物的结算时间可视为总体的一个容量为50的随机样本,将频率视为概率得,
P(X=0.5)=
=0.2,P(X=1)=
=0.4,P(X=1.5)=
=0.2,P(X=2)=
=0.1,P(X=2.5)=
=0.1.
所以X的分布列为
X的数学期望为EX=0.5×0.2+1×0.4+1.5×0.2+2×0.2+2.5×0.1=1.25.
(3)记“该顾客结算前的等候时间不超过2分钟”为事件A,该顾客前面第i位顾客的结算时间为Xi(i=1,2),由于各顾客的结算相互独立,且X1,X2的分布列都与X的分布列相同,所以
P(A)=P(X1=0.5)?P(X2=0.5)+P(X1=0.5)?P(X2=1)+P(X1=0.5)?P(X2=1.5)+P(X1=1)?P(X2=0.5)+P(X1=1)?P(X2=0.5)+P(X1=1)?P(X2=1)+P(X1=1.5)?P(X2=0.5)
=0.2×0.2+0.2×0.4+0.2×0.2+0.4×0.2+0.4×0.4+0.2×0.2=0.44 为所求.
(2)该超市所有顾客一次购物的结算时间组成一个总体,所以收集的50位顾客一次购物的结算时间可视为总体的一个容量为50的随机样本,将频率视为概率得,
P(X=0.5)=
| 10 |
| 50 |
| 20 |
| 50 |
| 10 |
| 50 |
| 5 |
| 50 |
| 5 |
| 50 |
所以X的分布列为
| X | 0.5 | 1 | 1.5 | 2 | 2.5 |
| P | 0.2 | 0.4 | 0.2 | 0.1 | 0.1 |
(3)记“该顾客结算前的等候时间不超过2分钟”为事件A,该顾客前面第i位顾客的结算时间为Xi(i=1,2),由于各顾客的结算相互独立,且X1,X2的分布列都与X的分布列相同,所以
P(A)=P(X1=0.5)?P(X2=0.5)+P(X1=0.5)?P(X2=1)+P(X1=0.5)?P(X2=1.5)+P(X1=1)?P(X2=0.5)+P(X1=1)?P(X2=0.5)+P(X1=1)?P(X2=1)+P(X1=1.5)?P(X2=0.5)
=0.2×0.2+0.2×0.4+0.2×0.2+0.4×0.2+0.4×0.4+0.2×0.2=0.44 为所求.
点评:本题主要考查概率与统计的内容,利用概率公式分别求出概率,然后求出概率的分布列,利用分布列求期望,考查学生的运算能力,综合性较强.

练习册系列答案
相关题目
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的50位顾客的相关数据,如下表所示:
|
一次购物量 |
1≤n≤3 |
4≤n≤6 |
7≤n≤9 |
10≤n≤12 |
n≥13 |
|
顾客数(人) |
|
20 |
10 |
5 |
|
|
结算时间(分钟/人) |
0.5 |
1 |
1.5 |
2 |
2.5 |
已知这50位顾客中一次购物量少于10件的顾客占80%.
(1)确定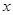 与
与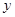 的值;
的值;
(2)若将频率视为概率,求顾客一次购物的结算时间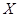 的分布列与数学期望;
的分布列与数学期望;
(3)在(2)的条件下,若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2分钟的概率.
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
|
一次购物量 |
1至4件 |
5至8件 |
9至12件 |
13至16件 |
17件及以上 |
|
顾客数(人) |
|
30 |
25 |
|
10 |
|
结算时间(分钟/人) |
1 |
1.5 |
2 |
2.5 |
3 |
已知这100位顾客中的一次购物量超过8件的顾客占55%.
(1)确定 的值,并求顾客一次购物的结算时间
的值,并求顾客一次购物的结算时间 的分布列与数学期望;
的分布列与数学期望;
(2)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过 分钟的概率.(注:将频率视为概率)
分钟的概率.(注:将频率视为概率)
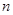 (件)
(件)