题目内容
已知p：-7≤x≤9，q：1-m≤x≤1+m（m＞0），若p是q的充分不必要条件，求m的取值范围．
分析：根据p是q的充分不必要条件，建立条件关系即可求m的取值范围．
解答：解：∵p是q的充分不必要条件，
∴p⇒q，q⇒p不成立，
∴
，
∴m≥8．
又q⇒p不成立，
∴m≠8，
故m∈（8，+∞）．
∴p⇒q，q⇒p不成立，
∴
|
∴m≥8．
又q⇒p不成立，
∴m≠8，
故m∈（8，+∞）．
点评：本题主要考查充分条件和必要条件的应用，注意区间端点值等号的取舍问题．
练习册系列答案
相关题目
已知函数f（x）=sin2xcosφ+cos2xsinφ，（x∈R），（z∈R）其中φ为实数，且f（x）≤f（
）对任意实数R恒成立，记p=f（
），q=f（
），r=f（
），则p、q、r的大小关系是（ ）
| 2π |
| 9 |
| 2π |
| 3 |
| 5π |
| 6 |
| 7π |
| 6 |
| A、r＜p＜q |
| B、q＜r＜p |
| C、p＜q＜r |
| D、q＜p＜r |
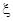的分布列如下：
的分布列如下：