题目内容
2.在数列{an}中,a1=2,且an+1=$\sqrt{\frac{{{a}^{2}}_{n}+1}{2}}$,求{an}的通项公式.分析 通过对an+1=$\sqrt{\frac{{{a}^{2}}_{n}+1}{2}}$两边同时平方、整理可知2(${{a}_{n+1}}^{2}$-1)=${{a}_{n}}^{2}$-1,进而可知数列{${{a}_{n}}^{2}$-1}是以3为首项、$\frac{1}{2}$为公比的等比数列,计算即得结论.
解答 解:依题意,an>0,
∵an+1=$\sqrt{\frac{{{a}^{2}}_{n}+1}{2}}$,
∴2${{a}_{n+1}}^{2}$=${{a}_{n}}^{2}$+1,
∴2(${{a}_{n+1}}^{2}$-1)=${{a}_{n}}^{2}$-1,
又∵${{a}_{1}}^{2}-1$=22-1=3,
∴数列{${{a}_{n}}^{2}$-1}是以3为首项、$\frac{1}{2}$为公比的等比数列,
∴${{a}_{n}}^{2}$-1=$\frac{3}{{2}^{n-1}}$,
∴an=$\sqrt{\frac{3+{2}^{n-1}}{{2}^{n-1}}}$.
点评 本题考查数列的通项,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
14.已知数列{an}的前n项的乘积为Tn=3${\;}^{{n}^{2}}$(n∈N*),则数列{an}的前n项的和为( )
| A. | $\frac{3}{2}$(3n-1) | B. | $\frac{9}{2}$(3n-1) | C. | $\frac{3}{8}$(9n-1) | D. | $\frac{9}{8}$(9n-1) |
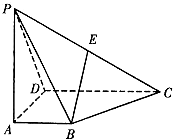 如图,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB=2,PA⊥底面ABCD,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB=2,PA⊥底面ABCD,E是PC的中点.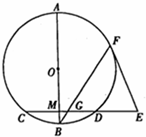 如图,AB是圆O的直径,弦CD⊥AB于点M,E是CD延长线上一点,AB=10,CD=8,3ED=4OM,EF切圆O于F,BF交CD于G.
如图,AB是圆O的直径,弦CD⊥AB于点M,E是CD延长线上一点,AB=10,CD=8,3ED=4OM,EF切圆O于F,BF交CD于G.