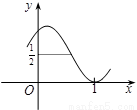题目内容
如果存在正整数ω和实数φ使得函数f(x)=cos2(ωx+φ)(ω,φ为常数)的图象如图所示(图象经过点(1,0)),那么ω的值为( )
A.1
B.2
C.3
D.4
【答案】分析:化简函数的表达式为一个角的三角函数的形式,通过周期的范围,确定ω的范围,利用图象经过点(1,0),以及 ,缩小ω的范围,根据ω为整数,求出ω的值.
,缩小ω的范围,根据ω为整数,求出ω的值.
解答:解:由f(x)=cos2(ωx+φ)= 及图象知:函数的半周期在(
及图象知:函数的半周期在( ,1)之间,即
,1)之间,即 得
得 ,正整数ω=2或3;
,正整数ω=2或3;
由图象经过点(1,0),所以 知2ω+2ϕ=(2k+1)π(k∈Z),2ω=-2ϕ+(2k+1)π
知2ω+2ϕ=(2k+1)π(k∈Z),2ω=-2ϕ+(2k+1)π
由图象知 ,
,
即 ,得cos2ω<0,又ω为正整数,所以ω=2,
,得cos2ω<0,又ω为正整数,所以ω=2,
故选B
点评:本题是基础题,考查三角函数的解析式的求法,周期的应用,图象的特殊点的应用,考查发现问题解决问题的能力.
 ,缩小ω的范围,根据ω为整数,求出ω的值.
,缩小ω的范围,根据ω为整数,求出ω的值.解答:解:由f(x)=cos2(ωx+φ)=
 及图象知:函数的半周期在(
及图象知:函数的半周期在( ,1)之间,即
,1)之间,即 得
得 ,正整数ω=2或3;
,正整数ω=2或3;由图象经过点(1,0),所以
 知2ω+2ϕ=(2k+1)π(k∈Z),2ω=-2ϕ+(2k+1)π
知2ω+2ϕ=(2k+1)π(k∈Z),2ω=-2ϕ+(2k+1)π由图象知
 ,
,即
 ,得cos2ω<0,又ω为正整数,所以ω=2,
,得cos2ω<0,又ω为正整数,所以ω=2,故选B
点评:本题是基础题,考查三角函数的解析式的求法,周期的应用,图象的特殊点的应用,考查发现问题解决问题的能力.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
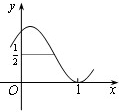
 如果存在正整数ω和实数φ,使得函数f(x)=cos2(ωx+φ)的图象如图所示,且图象经过点(1,0),那么ω的值为( )
如果存在正整数ω和实数φ,使得函数f(x)=cos2(ωx+φ)的图象如图所示,且图象经过点(1,0),那么ω的值为( ) 的图象如图所示(图象经过点(1,0)),那么
的图象如图所示(图象经过点(1,0)),那么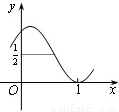
 和实数
和实数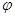 使得函数
使得函数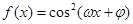 (
(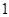 B.
B.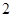 C. 3
D. 4
C. 3
D. 4