题目内容
【题目】已知定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,当
,当![]() 时
时![]() ,则关于函数
,则关于函数![]() 有如下四个结论:①
有如下四个结论:①![]() 为偶函数;②
为偶函数;②![]() 的图象关于直线
的图象关于直线![]() 对称;③方程
对称;③方程![]() 有两个不等实根;④
有两个不等实根;④![]() 其中所有正确结论的编号是_______.
其中所有正确结论的编号是_______.
【答案】①②
【解析】
由题意判断![]() 是周期函数,且为偶函数,由此判断所给的命题是否正确即可.
是周期函数,且为偶函数,由此判断所给的命题是否正确即可.
对于①,由题意知![]() ,所以
,所以![]() 是周期为2的函数;
是周期为2的函数;
当![]() 时,
时,![]() ,
,
所以![]() 为偶函数,①正确;
为偶函数,①正确;
对于②,![]() 是偶函数,对称轴是
是偶函数,对称轴是![]() ,又
,又![]() 是周期为2的函数,
是周期为2的函数,
所以![]() 的图象关于直线
的图象关于直线![]() 对称,②正确;
对称,②正确;
对于③,方程![]() 化为
化为![]() ,
,
设![]() ,则方程化为
,则方程化为![]() ;
;
由函数![]() 和
和![]() 的图象知,图象没有交点,方程无实数根,③错误;
的图象知,图象没有交点,方程无实数根,③错误;
对于④,![]() 是周期为2的函数,且为偶函数,在
是周期为2的函数,且为偶函数,在![]() 上是单调递减函数;
上是单调递减函数;
所以![]() ;
;
又![]() ,所以
,所以![]() ,
,
即![]() ,所以④错误.
,所以④错误.
综上知,正确的命题序号是①②.
故答案为:①②.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案【题目】随着运动app和手环的普及和应用,在朋友圈、运动圈中出现了每天1万步的健身打卡现象,“日行一万步,健康一辈子”的观念广泛流传.“健步达人”小王某天统计了他朋友圈中所有好友(共500人)的走路步数,并整理成下表:
分组(单位:千步) |
|
|
|
|
|
|
|
|
频数 | 60 | 240 | 100 | 60 | 20 | 18 | 0 | 2 |
(1)请估算这一天小王朋友圈中好友走路步数的平均数(同一组中数据以这组数据所在区间中点值作代表);
(2)若用![]() 表示事件“走路步数低于平均步数”,试估计事件
表示事件“走路步数低于平均步数”,试估计事件![]() 发生的概率;
发生的概率;
(3)若称每天走路不少于8千步的人为“健步达人”,小王朋友圈中岁数在40岁以上的中老年人共有300人,其中健步达人恰有150人,请填写下面![]() 列联表.根据列联表判断,有多大把握认为,健步达人与年龄有关?
列联表.根据列联表判断,有多大把握认为,健步达人与年龄有关?
健步达人 | 非健步达人 | 合计 | |
40岁以上 | |||
不超过40岁 | |||
合计 |
附: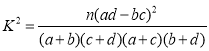 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】为了促进我国人口均衡发展,从2016年1月1日起,全国统一实施全面放开二孩政策,这也是为了重建大国人口观,重新认识人口价值、人口规律、人口问题,某研究机构为了了解人们对全面放开生育二孩政策的态度,随机调查了200人,得到的统计数据如下面的不完整的2×2列联表所示(单位:人):
支持生育二孩 | 不支持生育二孩 | 合计 | |
男性 | 30 | ||
女性 | 60 | 100 | |
合计 | 70 |
(1)完成2×2列联表,并求是否有90%的把握认为是否“支持生育二孩”与性别有关?
(2)现从样本中的女性中利用分层抽样的方法抽取5人,再从这5人中随机选出2人进行深层次的交流,求选出的2人中至少有1人“支持生育二孩”的概率.
参考公式: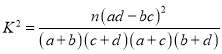 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】某省即将实行新高考,不再实行文理分科.某校为了研究数学成绩优秀是否对选择物理有影响,对该校2018级的1000名学生进行调查,收集到相关数据如下:
(1)根据以上提供的信息,完成![]() 列联表,并完善等高条形图;
列联表,并完善等高条形图;
选物理 | 不选物理 | 总计 | |
数学成绩优秀 | |||
数学成绩不优秀 | 260 | ||
总计 | 600 | 1000 |
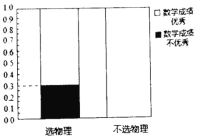
(2)能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关?
附: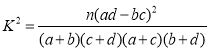
临界值表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |