题目内容
3.设|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=2,|$\overrightarrow{c}$|=5,向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{6}$,向量$\overrightarrow{b}$与$\overrightarrow{c}$的夹角为$\frac{π}{3}$,计算:(1)|($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$|;
(2)|$\overrightarrow{a}$•($\overrightarrow{b}$•$\overrightarrow{c}$)|
分析 (1)运用向量的数量积的定义,可得$\overrightarrow{a}$•$\overrightarrow{b}$,计算即可得到所求;
(2)运用向量的数量积的定义,可得$\overrightarrow{b}$•$\overrightarrow{c}$,计算即可得到所求.
解答 解:(1)$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cos$\frac{π}{6}$=3×2×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
则|($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$|=3$\sqrt{3}$|$\overrightarrow{c}$|=3$\sqrt{3}$×5=15$\sqrt{3}$;
(2)$\overrightarrow{b}$•$\overrightarrow{c}$=|$\overrightarrow{b}$|•|$\overrightarrow{c}$|•cos$\frac{π}{3}$=2×5×$\frac{1}{2}$=5,
则|$\overrightarrow{a}$•($\overrightarrow{b}$•$\overrightarrow{c}$)|=5|$\overrightarrow{a}$|=5×3=15.
点评 本题考查向量的数量积的定义,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
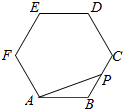 如图所示:点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间[-8,24].
如图所示:点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间[-8,24].