题目内容
在锐角三角形ABC中,a、b、c分别是角A、B、C的对边,
且 .
.
(Ⅰ)求角 的大小; (Ⅱ)若
的大小; (Ⅱ)若 的最大值.
的最大值.
解:(Ⅰ)由 a-2csin A=0及正弦定理,
a-2csin A=0及正弦定理,
得 sin A-2sin Csin A=0(sin A≠0),(1分)
sin A-2sin Csin A=0(sin A≠0),(1分)
∴sin C= ,(4分)∵△ABC是锐角三角形,
,(4分)∵△ABC是锐角三角形,
∴C= (6分)
(6分)
(Ⅱ)∵c=2,C= ,由余弦定理,a2+b2-2abcos
,由余弦定理,a2+b2-2abcos  =4,
=4,
即a2+b2-ab=4 (8分)
∴(a+b)2=4+3ab≤4+3· 2,即(a+b)2≤16,(10分)
2,即(a+b)2≤16,(10分)
∴a+b≤4,当且仅当a=b=2取“=”(11分)
故a+b的最大值是4.(12分)

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 ,则
,则 ( )
( )
 B.
B. C.
C. D.
D.
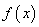 在
在 上可导,
上可导, ,则
,则 .
. 等于( )
等于( ) B.
B. C.
C. D.
D.
 相切的一条直线的方程为( )
相切的一条直线的方程为( ) B.
B.
 D.
D.
 在
在 处的切线
处的切线 与直线
与直线 垂直,函数
垂直,函数 .
. 的值;
的值; 存在单调递减区间,求实数b的取值范围;
存在单调递减区间,求实数b的取值范围; 是函数
是函数 ,求
,求 的最小值.
的最小值.