题目内容
如图,在正四棱柱ABCD—A1B(1)异面直线AD与C
(2)二面角A—C
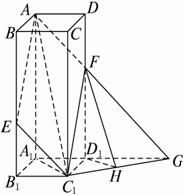
解法一:(1)由AD∥D
如图,连结C![]() .再由△FD
.再由△FD![]() .
.

在Rt△C1D![]() 得∠C1GD1=+
得∠C1GD1=+![]() .
.
(2)作D1H⊥C
在Rt△GHD1中,由D![]() ,∠D1GH=
,∠D1GH=![]() 得D1H=
得D1H=![]() ,从而tanD1HF=
,从而tanD1HF= =2.
=2.
解法二:(1)由AD∥D
因为EC1和AF是平行平面BB
由此可得∠AGA1=∠EC1B1=![]() ,
,
从而A![]() +1,于是D
+1,于是D![]() .
.
在Rt△C1D![]() 得∠C1GD1=
得∠C1GD1=![]() .
.
(2)在△A![]() ,∠A1GC1=
,∠A1GC1=![]() 知∠A
知∠A

在Rt△A1HG中,由 A![]() ,∠A1GH=
,∠A1GH=![]() 得A1H=
得A1H=![]() .
.
从而tanAHA1= =2.
=2.

练习册系列答案
相关题目
 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
 如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=4,AB=2,E是棱CC1上的一个动点.
如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=4,AB=2,E是棱CC1上的一个动点. (2012•青岛一模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,
(2012•青岛一模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=a, 如图,在正四棱柱ABCD-A1B1C1D1中,AA1=A(x0,y0)AB=2,点E、M分别为A1B、C1C的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AA1=A(x0,y0)AB=2,点E、M分别为A1B、C1C的中点. (2009•宜昌模拟)如图,在正四棱柱ABCD-A1B1C1D1 中,AB=BC=1,AA1=2.过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于60°,这样的直线l最多可作( )
(2009•宜昌模拟)如图,在正四棱柱ABCD-A1B1C1D1 中,AB=BC=1,AA1=2.过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于60°,这样的直线l最多可作( )