题目内容
(1)若a>0,b>0,求证:![]() ≥a+b.
≥a+b.
(2)设a、b、c都是正数,求证:![]() ≥
≥![]() (a+b+c).
(a+b+c).
(1)思路分析:主要利用不等式![]() ≥
≥![]() 和a2+b2≥2ab.
和a2+b2≥2ab.
证明:由a2+b2≥2ab,
∴2(a2+b2)≥a2+b2+2ab,即2(a2+b2)≥(a+b)2.
∴![]() ≥
≥![]() ≥
≥![]() =a+b.
=a+b.
(2)思路分析:主要利用不等式![]() ≥
≥![]() .
.
证明:由不等式a2+b2≥![]() .∴
.∴![]() ≥
≥![]() .
.
同理,![]() ≥
≥![]() ,
,![]() ≥
≥![]() .
.
∴![]() +
+![]() +
+![]()
=![]() (
(![]() +
+![]() +
+![]() )
)
=![]() (a+b+c).
(a+b+c).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
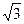 为
为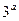 与
与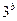 的等比中项,求
的等比中项,求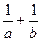 的最小值
的最小值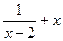 的值域.
的值域. 若
若
 =
=