题目内容
1.设曲线C的参数方程为$\left\{\begin{array}{l}x=2+3cosθ\\ y=-1+3sinθ\end{array}\right.$(θ为参数),直线l的方程为ρcosθ-3ρsinθ+2=0,则曲线C上到直线l距离为$\frac{{7\sqrt{10}}}{10}$的点的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 曲线C的参数方程为$\left\{\begin{array}{l}x=2+3cosθ\\ y=-1+3sinθ\end{array}\right.$(θ为参数),化为(x-2)2+(y+1)2=9.直线l的方程为ρcosθ-3ρsinθ+2=0,化为直角坐标方程.求出圆心C(2,-1)到直线l的距离d,与半径比较大小即可得出.
解答 解:曲线C的参数方程为$\left\{\begin{array}{l}x=2+3cosθ\\ y=-1+3sinθ\end{array}\right.$(θ为参数),化为(x-2)2+(y+1)2=9.
直线l的方程为ρcosθ-3ρsinθ+2=0,化为直角坐标方程为:x-3y+2=0.
圆心C(2,-1)到直线l的距离d=$\frac{|2+3+2|}{\sqrt{10}}$=$\frac{7\sqrt{10}}{10}$<3=R,且R-d=3-$\frac{7\sqrt{10}}{10}$<R,
则曲线C上到直线l距离为$\frac{{7\sqrt{10}}}{10}$的点的个数为2.
故选:B.
点评 本题考查了圆的参数化为普通方程、极坐标方程化为直角坐标方程、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
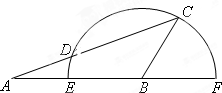 如图,在△ABC中,AB=5,BC=3,∠ABC=120°,以点B为圆心,线段BC的长为半径的半圆交AB所在直线于点E、F,交线段AC于点D,则线段AD的长为$\frac{16}{7}$.
如图,在△ABC中,AB=5,BC=3,∠ABC=120°,以点B为圆心,线段BC的长为半径的半圆交AB所在直线于点E、F,交线段AC于点D,则线段AD的长为$\frac{16}{7}$.