题目内容
满足A=60°,c=1,a=
的△ABC的个数记为m,则am的值为( )
| 3 |
分析:由余弦定理可得b的值只有一个,即m=1,由此可得am的值.
解答:解:由余弦定理可得 a2=b2+c2-2bc•cosA,
即 3=b2+1-2b•
,解得 b=2,或b=-1(舍去).
由于b只有一个值,故三角形有一个解,即m=1,∴am=
,
故选B.
即 3=b2+1-2b•
| 1 |
| 2 |
由于b只有一个值,故三角形有一个解,即m=1,∴am=
| 3 |
故选B.
点评:本题主要考查余弦定理的应用,判断三角形的解的个数,属于中档题.

练习册系列答案
相关题目
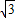 的△ABC的个数记为m,则am的值为( )
的△ABC的个数记为m,则am的值为( )