题目内容
已知函数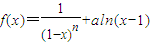 ,其中n∈N*,a为常数.
,其中n∈N*,a为常数.(Ⅰ)当n=2时,求函数f(x)的极值;
(Ⅱ)当a=1时,证明:对任意的正整数n,当x≥2时,有f(x)≤x-1.
【答案】分析:(1)欲求:“当n=2时, ”的极值,利用导数,求其导函数的零点及单调性进行判断即可;
”的极值,利用导数,求其导函数的零点及单调性进行判断即可;
(2)欲证:“f(x)≤x-1”,令 ,利用导函数的单调性,只要证明函数f(x)的最大值是x-1即可.
,利用导函数的单调性,只要证明函数f(x)的最大值是x-1即可.
解答:解:(Ⅰ)解:由已知得函数f(x)的定义域为{x|x>1},
当n=2时, ,所以
,所以 .
.
(1)当a>0时,由f'(x)=0得 ,
, ,
,
此时 .
.
当x∈(1,x1)时,f'(x)<0,f(x)单调递减;
当x∈(x1,+∞)时,f'(x)>0,f(x)单调递增.
(2)当a≤0时,f'(x)<0恒成立,所以f(x)无极值.
综上所述,n=2时,
当a>0时,f(x)在 处取得极小值,极小值为
处取得极小值,极小值为 .
.
当a≤0时,f(x)无极值.
(Ⅱ)证法一:因为a=1,所以 .
.
当n为偶数时,
令 ,
,
则 (x≥2).
(x≥2).
所以当x∈[2,+∞)时,g(x)单调递增,
又g(2)=0,
因此 恒成立,
恒成立,
所以f(x)≤x-1成立.
要证f(x)≤x-1,由于 ,所以只需证ln(x-1)≤x-1,
,所以只需证ln(x-1)≤x-1,
令h(x)=x-1-ln(x-1),
则 (x≥2),
(x≥2),
所以当x∈[2,+∞)时,h(x)=x-1-ln(x-1)单调递增,又h(2)=1>0,
所以当x≥2时,恒有h(x)>0,即ln(x-1)<x-1命题成立.
综上所述,结论成立.
证法二:当a=1时, .
.
当x≥2时,对任意的正整数n,恒有 ,
,
故只需证明1+ln(x-1)≤x-1.
令h(x)=x-1-(1+ln(x-1))=x-2-ln(x-1),x∈[2,+∞),
则 ,
,
当x≥2时,h'(x)≥0,故h(x)在[2,+∞)上单调递增,
因此当x≥2时,h(x)≥h(2)=0,即1+ln(x-1)≤x-1成立.
故当x≥2时,有 .
.
即f(x)≤x-1.
点评:本题主要考查函数的导数、不等式等知识,以及不等式的证明,同时考查逻辑推理能力.
 ”的极值,利用导数,求其导函数的零点及单调性进行判断即可;
”的极值,利用导数,求其导函数的零点及单调性进行判断即可;(2)欲证:“f(x)≤x-1”,令
 ,利用导函数的单调性,只要证明函数f(x)的最大值是x-1即可.
,利用导函数的单调性,只要证明函数f(x)的最大值是x-1即可.解答:解:(Ⅰ)解:由已知得函数f(x)的定义域为{x|x>1},
当n=2时,
 ,所以
,所以 .
.(1)当a>0时,由f'(x)=0得
 ,
, ,
,此时
 .
.当x∈(1,x1)时,f'(x)<0,f(x)单调递减;
当x∈(x1,+∞)时,f'(x)>0,f(x)单调递增.
(2)当a≤0时,f'(x)<0恒成立,所以f(x)无极值.
综上所述,n=2时,
当a>0时,f(x)在
 处取得极小值,极小值为
处取得极小值,极小值为 .
.当a≤0时,f(x)无极值.
(Ⅱ)证法一:因为a=1,所以
 .
.当n为偶数时,
令
 ,
,则
 (x≥2).
(x≥2).所以当x∈[2,+∞)时,g(x)单调递增,
又g(2)=0,
因此
 恒成立,
恒成立,所以f(x)≤x-1成立.
要证f(x)≤x-1,由于
 ,所以只需证ln(x-1)≤x-1,
,所以只需证ln(x-1)≤x-1,令h(x)=x-1-ln(x-1),
则
 (x≥2),
(x≥2),所以当x∈[2,+∞)时,h(x)=x-1-ln(x-1)单调递增,又h(2)=1>0,
所以当x≥2时,恒有h(x)>0,即ln(x-1)<x-1命题成立.
综上所述,结论成立.
证法二:当a=1时,
 .
.当x≥2时,对任意的正整数n,恒有
 ,
,故只需证明1+ln(x-1)≤x-1.
令h(x)=x-1-(1+ln(x-1))=x-2-ln(x-1),x∈[2,+∞),
则
 ,
,当x≥2时,h'(x)≥0,故h(x)在[2,+∞)上单调递增,
因此当x≥2时,h(x)≥h(2)=0,即1+ln(x-1)≤x-1成立.
故当x≥2时,有
 .
.即f(x)≤x-1.
点评:本题主要考查函数的导数、不等式等知识,以及不等式的证明,同时考查逻辑推理能力.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目

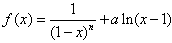 ,其中n∈N*,a为常数。
,其中n∈N*,a为常数。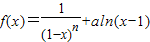 ,其中n∈N*,a为常数.
,其中n∈N*,a为常数.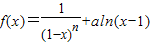 ,其中n∈N*,a为常数.
,其中n∈N*,a为常数.