题目内容
(1)(如图)在底半径为 ,母线长为
,母线长为 的圆锥中内接一个高为
的圆锥中内接一个高为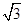 的圆柱,求圆柱的表面积
的圆柱,求圆柱的表面积

(2)如图,在四边形 中,
中, ,
, ,
, ,
, ,
, ,求四边形
,求四边形 绕
绕 旋转一周所成几何体的表面积及体积.
旋转一周所成几何体的表面积及体积.
 ,母线长为
,母线长为 的圆锥中内接一个高为
的圆锥中内接一个高为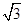 的圆柱,求圆柱的表面积
的圆柱,求圆柱的表面积
(2)如图,在四边形
 中,
中, ,
, ,
, ,
, ,
, ,求四边形
,求四边形 绕
绕 旋转一周所成几何体的表面积及体积.
旋转一周所成几何体的表面积及体积.
解:(1)
(2)




(2)




本题考查的知识点是圆柱的表面积,圆台的体积问题,其中根据已知条件,求出圆柱的底面半径,是解答本题的关键
(1)由已知中底面半径为2母线长为4的圆锥中内接一个高为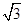 的圆柱,我们可计算出圆柱的底面半径,代入圆柱表面积公式,即可得到答案
的圆柱,我们可计算出圆柱的底面半径,代入圆柱表面积公式,即可得到答案
(2)旋转后的几何体是圆台除去一个倒放的圆锥,根据题目所给数据,求出圆台的侧面积、圆锥的侧面积、圆台的底面积,即可求出几何体的表面积.求出圆台体积减去圆锥体积,即可得到几何体的体积.
(1)由已知中底面半径为2母线长为4的圆锥中内接一个高为
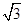 的圆柱,我们可计算出圆柱的底面半径,代入圆柱表面积公式,即可得到答案
的圆柱,我们可计算出圆柱的底面半径,代入圆柱表面积公式,即可得到答案(2)旋转后的几何体是圆台除去一个倒放的圆锥,根据题目所给数据,求出圆台的侧面积、圆锥的侧面积、圆台的底面积,即可求出几何体的表面积.求出圆台体积减去圆锥体积,即可得到几何体的体积.

练习册系列答案
相关题目
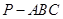 中,
中, 底面
底面 , 点
, 点 ,
, 分别在棱
分别在棱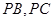 上,且
上,且

 平面
平面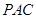 ;
; 的中点时,求
的中点时,求 与平面
与平面





 内有一个球与正方体的各个面都相切,经过
内有一个球与正方体的各个面都相切,经过 和
和 作一个截面,正确的截面图是 .
作一个截面,正确的截面图是 .



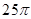

 ,则a=________.
,则a=________.
