题目内容
(本题满分12分)
已知椭圆![]() 、抛物线
、抛物线![]() 的焦点均在
的焦点均在![]() 轴上,
轴上,![]() 的中心和
的中心和![]() 的顶点均为原点
的顶点均为原点![]() ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
|
| 3 |
| 4 |
|
|
|
| 0 |
|
|
(Ⅰ)求![]() 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线![]() 满足条件:①过
满足条件:①过![]() 的焦点
的焦点![]() ;②与
;②与![]() 交不同两点
交不同两点![]() 且满足
且满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
解:(Ⅰ)设抛物线![]() ,则有
,则有![]() ,据此验证
,据此验证![]() 个点知(3,
个点知(3,![]() )、(4,
)、(4,![]() 4)在抛物线上,易求
4)在抛物线上,易求![]() ………………2分
………………2分
设![]() :
:![]() ,把点(
,把点(![]() 2,0)(
2,0)(![]() ,
,![]() )代入得:
)代入得:
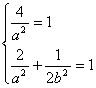 解得
解得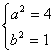
∴![]() 方程为
方程为![]() ………………………………………………………………5分
………………………………………………………………5分
(Ⅱ)法一:
假设存在这样的直线![]() 过抛物线焦点
过抛物线焦点![]() ,设直线
,设直线![]() 的方程为
的方程为![]() 两交点坐标为
两交点坐标为![]() ,
,
由 消去
消去![]() ,得
,得![]() …………………………7分
…………………………7分
∴![]() ①
①
![]()
![]() ② ………………………9分
② ………………………9分
由![]() ,即
,即![]() ,得
,得![]()
将①②代入(*)式,得![]() , 解得
, 解得![]() …………………11分
…………………11分
所以假设成立,即存在直线![]() 满足条件,且
满足条件,且![]() 的方程为:
的方程为:![]() 或
或![]() …………………………………………………………………………………12分
…………………………………………………………………………………12分
法二:容易验证直线![]() 的斜率不存在时,不满足题意;……………………………6分
的斜率不存在时,不满足题意;……………………………6分
当直线![]() 斜率存在时,假设存在直线
斜率存在时,假设存在直线![]() 过抛物线焦点
过抛物线焦点![]() ,设其方程为
,设其方程为![]() ,与
,与![]() 的交点坐标为
的交点坐标为![]()
由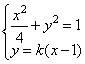 消掉
消掉![]() ,得
,得 ![]() , …………8分
, …………8分
于是 ![]() ,
,![]() ①
①
![]()
即![]() ② ………………………………10分
② ………………………………10分
由![]() ,即
,即![]() ,得
,得![]()
将①、②代入(*)式,得 ![]() ,解得
,解得![]() ;……11分
;……11分
所以存在直线![]() 满足条件,且
满足条件,且![]() 的方程为:
的方程为:![]() 或
或![]() .………12分
.………12分

练习册系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面