题目内容
下图是两个全等的正三角形.给定下列三个命题:①存在四 棱锥,其正视图、侧视图如右图;②存在三棱锥,其正视图、侧视图如右图;③存在圆锥,其正视图、侧视图如右图.其中 真命题的个数是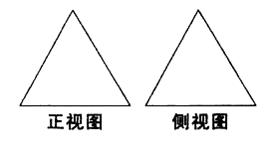
| A.3 | B.2 | C.1 | D.O |
A
解析试题分析:对于①存在四棱锥,其正视图、侧视图,这时的四棱锥是正四棱锥可以满足题意。
②存在三棱锥,其正视图、侧视图,那么对于正四面体符合题意。
③存在圆锥,其正视图、侧视图只要底面的圆的直径和侧棱长相等则符合题意。故选A.
考点:本试题考查了三视图的知识点。
点评:解决该试题的关键是对于特殊的几何体的三视图的准确理解和运用。同时要通过不同的摆放来实现三视图,这是试题的一个难点,属于中档题。

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
已知一个棱长为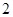 的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的体积是
的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的体积是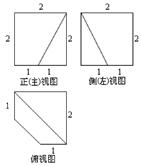
| A.8 | B.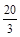 |
C.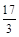 | D.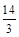 |
已知某四棱锥的三视图(单位:cm)如图所示,则该四棱锥的体积是
A. | B. | C. | D.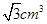 |
一个几何体的三视图如图所示,则该几何体的体积为( )
| A.25 | B.36 | C.12 | D.24 |
棱长为1的正方体的外接球的表面积为
A. | B. | C. | D. |
一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形. 则该几何体的体积为( )
| A.16 | B.48 |
| C.60 | D.96 |
已知一个几何体的三视图如图所示,则该几何体的体积是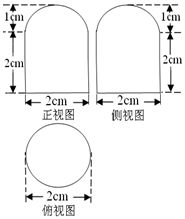
A. | B. |
C. | D. |


 的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去
的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去 个三棱锥后 ,剩下的几何体的体积是( )
个三棱锥后 ,剩下的几何体的体积是( )


