题目内容
在共有2 013项的等差数列{an}中,有等式(a1+a3+…+a2013)-(a2+a4+…+a2012)=a1007成立;类比上述性质,在共有2 013项的等比数列{bn}中,相应的有等式 成立.
【答案】分析:仔细分析题干中给出的不等式的结论:(a1+a3+…+a2013)-(a2+a4+…+a2012)=a1007的规律,结合等差数列与等比数列具有类比性,且等差数列与和差有关,等比数列与积商有关,因此等差数列类比到等比数列的: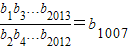 成立.
成立.
解答:解:等差数列中的bn和am可以类比等比数列中的bn和am,
等差数列中的bn-am可以类比等比数列中的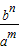 ,
,
等差数列中的“差”可以类比等比数列中的“商”.
故等式(a1+a3+…+a2013)-(a2+a4+…+a2012)=a1007成立,类比得到性质: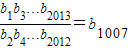
故答案为: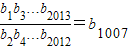 .
.
点评:本题考查类比推理、等差,等比数列的性质.掌握类比推理的规则及类比对象的特征是解本题的关键,本题中由等差结论类比等比结论,其运算关系由加类比乘,由减类比除,解题的难点是找出两个对象特征的对应,作出合乎情理的类比.
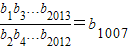 成立.
成立.解答:解:等差数列中的bn和am可以类比等比数列中的bn和am,
等差数列中的bn-am可以类比等比数列中的
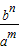 ,
,等差数列中的“差”可以类比等比数列中的“商”.
故等式(a1+a3+…+a2013)-(a2+a4+…+a2012)=a1007成立,类比得到性质:
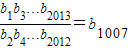
故答案为:
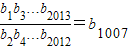 .
.点评:本题考查类比推理、等差,等比数列的性质.掌握类比推理的规则及类比对象的特征是解本题的关键,本题中由等差结论类比等比结论,其运算关系由加类比乘,由减类比除,解题的难点是找出两个对象特征的对应,作出合乎情理的类比.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目