题目内容
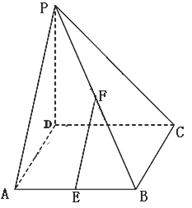
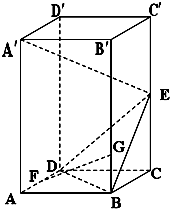
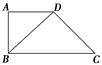
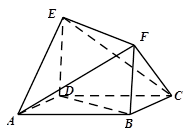
如图,在四棱锥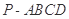 中,
中,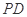 ⊥底面
⊥底面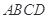 ,底面
,底面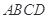
为正方形,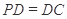 ,
, ,
, 分别是
分别是 ,
,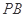 的 中点.
的 中点.
(1)求证: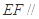 平面
平面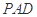 ;
;
(2)求证: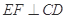 ;
;
(3)若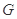 是线段
是线段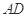 上一动点,试确定
上一动点,试确定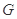 点位置,
点位置,
使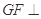 平面
平面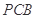 ,并证明你的结论.
,并证明你的结论.
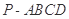 中,
中,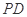 ⊥底面
⊥底面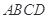 ,底面
,底面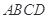
为正方形,
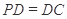 ,
,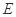 ,
,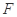 分别是
分别是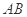 ,
,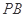 的 中点.
的 中点.(1)求证:
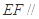 平面
平面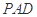 ;
;(2)求证:
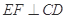 ;
;(3)若
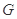 是线段
是线段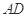 上一动点,试确定
上一动点,试确定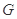 点位置,
点位置,使
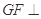 平面
平面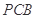 ,并证明你的结论.
,并证明你的结论.
(1)详见解析;(2) 详见解析; (3)G是线段AD的中点.
试题分析:(1)证线面平行主要是利用线面平行的判定定理,其关键是找到面内直线与该直线平行,并要注明所证直线在面外的;2)证明线线垂直主要是转化为直线与平面垂直来证明的,而直线与平面垂直的证明又主要是通过证明直线与平面内的两条相交直线都垂直来实现的,再注意一直线垂直两平行线中的一条必垂直于另一条;(3)先由图形直观分析出点G应为线段AD的中点,再证明.
试题解析:(1)证明:
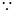
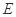 ,
,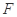 分别是
分别是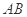 ,
,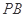 的 中点,
的 中点,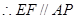 ,又
,又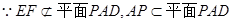 ,
,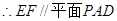 .
.(2)因为四边形ABCD为正方形,
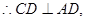 又
又 ,
,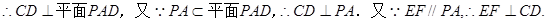
(3)G是线段AD的中点时,GF
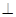 平面PCB.证明如下:
平面PCB.证明如下:取BC的中点为H,连结DH,HF;
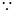 PD=PC,
PD=PC,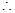 DH
DH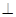 PC;又
PC;又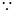 BC
BC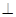 平面PDC,
平面PDC,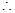 BC
BC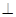 DH,
DH,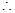 DH
DH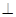 平面PCB.
平面PCB.又
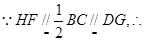 四边形DGFH为平行四边形,
四边形DGFH为平行四边形,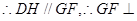 平面PCB.
平面PCB.
练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
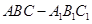 中,
中,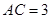 ,
,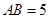 ,
,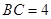 ,
,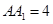 ,点
,点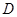 是
是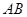 的中点.
的中点.
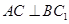 ;
; 
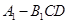 的体积.
的体积.
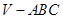 中,
中,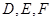 分别是
分别是 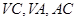 的中点,
的中点,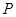 为
为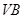 上任意一点,则直线
上任意一点,则直线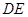 与
与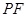 所成的角的大小是 ( )
所成的角的大小是 ( )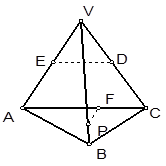
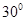
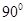
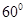

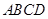 是菱形,
是菱形,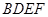 是矩形,
是矩形,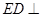 面
面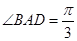 .
.
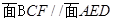 ;
;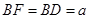 ,求四棱锥
,求四棱锥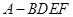 的体积.
的体积.