题目内容
【题目】已知函数
.
⑴求函数
的单调区间；
⑵如果对于任意的
, 
恒成立，求实数
的取值范围；
⑶设函数
， 
.过点
作函数
的图象
的所有切线，令各切点的横坐标构成数列
，求数列
的所有项之和
的值.
【答案】⑴增区间为
；减区间为
;⑵
;⑶
.
【解析】试题分析：(1)求出函数的导函数,由导函数大于0求其增区间,导函数小于0求其减区间;
(2)构造辅助函数
,把问题转化为求
时
,然后对k的值进行分类讨论,求k在不同取值范围内时的
的最小值,由最小值大于等于0得到k的取值范围;
(3)把
的解析式代入
,求出函数
的导函数,设出切点坐标,求出函数在切点处的导数,由点斜式写出切线方程,把M的坐标代入切线方程,得到关于切点横坐标的三角方程,利用函数图象交点分析得到切点的横坐标关于
对称成对出现,最后由给出的自变量的范围得到数列
的所有项之和S的值.
试题分析：⑴
的增区间为
；减区间为
.
⑵令
,要使
恒成立，只需当
时， 
,令
，则
对
恒成立
在
上是增函数，则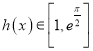
①当
时， 
恒成立， 
在
上为增函数
， 
满足题意；
②当
时， 
在
上有实根
, 
在
上是增函数
则当
时， 
， 
不符合题意；
③当
时， 
恒成立， 
在
上为减函数，
不符合题意
，即
.
⑶
设切点坐标为
，则切线斜率为
从而切线方程为
令
， 
，这两个函数的图象均关于点
对称，则它们交点的横坐标也关于
对称，从而所作的所有切线的切点的横坐标构成数列
的项也关于
成对出现，又在
共有1008对，每对和为
.
.
练习册系列答案
相关题目
