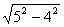Question

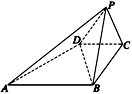
如图,直角梯形ABCD,AB⊥AD,BC∥AD,SA⊥平面ABCD,且SA=AB=BC=a,AD=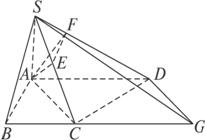2a.

(1)求证:平面CSD⊥平面SAC;

(2)求点A到平面SCD的距离;

(3)求二面角ASDC的大小;

(4)求直线SD与AC所成的角.

Answer 1

(1)证明:由∠ABC=90°,得AC=a,CD=a,AC²+CD²=AD².

∴∠ACD=90°.

又SA⊥CD,

∴CD⊥平面SAC.

∴平面DSC⊥平面SAC.

(2)解析:过点A作AE⊥SC,E为垂足,则AE⊥平面SCD,SC=a.

∴AE=,即A到平面SCD的距离为a.

(3)解析:作EF⊥SD,垂足为F,则AF⊥SD.∴∠AFE为二面角A-SD-C的平面角.

又AE⊥EF,SD=a,

AF=,

∴sin∠AFE=,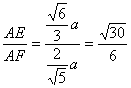

即二面角A-SD-C为arcsin.

(4)解析:延长BC至G,使GC=2a,则四边形ACGD为平行四边形,∠SDG为SD与AC所成的角(或补角).DG=AC=a,AG=a,SG=a,

cos∠SDG=,

∴SD与AC所成的角为arccos.