题目内容
抛物线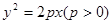 的焦点为
的焦点为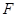 ,其上的动点
,其上的动点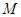 在准线上的射影为
在准线上的射影为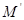 ,若
,若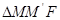 是等边三角形,则
是等边三角形,则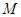 的横坐标是( )
的横坐标是( )
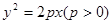 的焦点为
的焦点为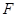 ,其上的动点
,其上的动点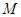 在准线上的射影为
在准线上的射影为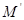 ,若
,若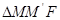 是等边三角形,则
是等边三角形,则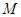 的横坐标是( )
的横坐标是( )A.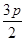 | B.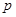 | C.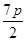 | D.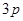 |
A
试题分析:设准线与
 轴的交点为P,在
轴的交点为P,在 中,
中, ,所以
,所以 ,所以
,所以 .
.点评:抛物线上的点到焦点的距离等于到准线的距离,这条性质非常重要,而且经常应用,要牢固掌握.

练习册系列答案
相关题目
题目内容
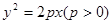 的焦点为
的焦点为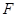 ,其上的动点
,其上的动点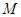 在准线上的射影为
在准线上的射影为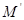 ,若
,若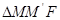 是等边三角形,则
是等边三角形,则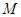 的横坐标是( )
的横坐标是( )A.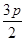 | B.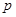 | C.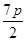 | D.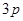 |
 轴的交点为P,在
轴的交点为P,在 中,
中, ,所以
,所以 ,所以
,所以 .
.