题目内容
3.若函数f(x)=$\left\{\begin{array}{l}{-2x+1,x<0}\\{g(x),x>0}\end{array}\right.$是奇函数,则f-1(x)=$\left\{\begin{array}{l}{\frac{1-x}{2},x>1}\\{-\frac{x+1}{2},x<-1}\end{array}\right.$.分析 由奇函数的性质求出f(x)=$\left\{\begin{array}{l}{-2x+1,x<0}\\{-2x-1,x>0}\end{array}\right.$,由此能求出f-1(x).
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{-2x+1,x<0}\\{g(x),x>0}\end{array}\right.$是奇函数,
∴x>0时,g(x)=-f(-x)=-[-2(-x)+1]=-2x-1,
∴f(x)=$\left\{\begin{array}{l}{-2x+1,x<0}\\{-2x-1,x>0}\end{array}\right.$,
当x<0时,y=f(x)=-2x+1,x=$\frac{1-y}{2}$,∴f-1(x)=$\frac{1-x}{2}$,x>1,
当x>0时,y=f(x)=-2x-1,x=-$\frac{y+1}{2}$,∴f-1(x)=-$\frac{x+1}{2}$,x<-1.
∴f-1(x)=$\left\{\begin{array}{l}{\frac{1-x}{2},x>1}\\{-\frac{x+1}{2},x<-1}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{\frac{1-x}{2},x>1}\\{-\frac{x+1}{2},x<-1}\end{array}\right.$.
点评 本题考查分段函数的反函数的求法,是基础题,解题时要认真审题,注意反函数的性质的合理运用.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
13.已知不等式组$\left\{\begin{array}{l}3x+4y-10≥0\\ x≤4\\ y≤3\end{array}\right.$表示区域D,过区域D中任意一点P作圆x2+y2=1的两条切线且切点分别为A,B,当∠PAB最小时,cos∠PAB=( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{{\sqrt{3}}}{2}$ | D. | -$\frac{1}{2}$ |
14.在平面直角坐标系内,以原点O为顶点,x轴非负半轴为始边,任作一角,该角的终边OA落在第一象限的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
11.下列命题中,正确的是( )
| A. | 如果直线l与平面α内无数条直线成异面直线,则l∥α | |
| B. | 如果直线l与平面α内无数条直线平行,则l∥α | |
| C. | 如果直线l与平面α内无数条直线成异面直线,则l?α | |
| D. | 如果一条直线与一个平面平行,则该直线平行于这个平面内的所有直线 | |
| E. | 如果一条直线上有无数个点不在平面内,则这条直线与这个平面平行 |
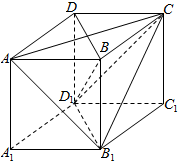 如图,棱长为1的正方体ABCD-A1B1C1D1中,
如图,棱长为1的正方体ABCD-A1B1C1D1中,