题目内容
a、b为常数,
解法一:由于![]() (a
(a![]() -bn)
-bn)
=![]()
![]()
=![]()
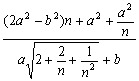 =1,
=1,
∴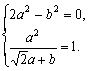 ∴a=2
∴a=2![]() ,b=4.
,b=4.
解法二:由已知![]() n(a
n(a![]() )=1,
)=1,
从而![]() [n(a
[n(a![]() )]存在极限.
)]存在极限.
![]()
![]() [n(a
[n(a![]() -b)]
-b)]
=![]()
![]() ·
·![]() n(a
n(a![]() -b)
-b)
=0×1=0,
∴![]() (a
(a![]() -b)=0.
-b)=0.
∴![]() a-b=0.
a-b=0.
又![]() (a
(a![]() -bn)
-bn)
=![]() (a
(a![]() -
-![]() an)
an)
=![]() a·
a·![]()
=a·![]()
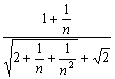 =
=![]() =1,
=1,
∴a=2![]() ,b=4.
,b=4.
点评:解法一的主要步骤是“分子有理化”.解法二利用了“若![]()
![]() [nf(n)]=0,则
[nf(n)]=0,则![]() f(n)=0”这一结论.
f(n)=0”这一结论.

练习册系列答案
相关题目