题目内容
求函数f（x）=x2e-x的极值。
解：函数的定义域为R，
f′（x）=2xe-x+x2·e-x·（-x）′
=2xe-x-x2e-x=x（2-x）e-x，
令f′（x）=0，即x（2-x）·e-x=0；
得x=0或x=2，
当x变化时f′（x），f（x）的变化情况如下表：
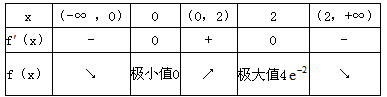
因此，当x=0时f（x）有极小值，并且极小值为f（0）=0；
当x=2时，f（x）有极大值，并且极大值为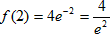
。
f′（x）=2xe-x+x2·e-x·（-x）′
=2xe-x-x2e-x=x（2-x）e-x，
令f′（x）=0，即x（2-x）·e-x=0；
得x=0或x=2，
当x变化时f′（x），f（x）的变化情况如下表：
因此，当x=0时f（x）有极小值，并且极小值为f（0）=0；
当x=2时，f（x）有极大值，并且极大值为
。 
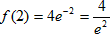练习册系列答案
53随堂测系列答案
相关题目
要解决下面四个问题，只用顺序结构画不出其程序框图的是（ ）
A、利用1+2+…+n=
| ||
| B、当图面积已知时，求圆的周长 | ||
| C、当给定一个数x，求其绝对值 | ||
| D、求函数f（x）=x2-4x+5的函数值 |