题目内容
下列命题中,真命题是( )
A. |
B. 是 是 的充要条件 的充要条件 |
C.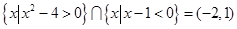 |
D.命题 的否定是真命题 的否定是真命题 |
D
解析试题分析:因为 的值恒大于零.所以A选项不正确.由
的值恒大于零.所以A选项不正确.由 可得
可得 所以充分性成立.但是
所以充分性成立.但是 不能推出
不能推出 .所以必要性不成立.即B选项不正确.由
.所以必要性不成立.即B选项不正确.由 可得x<-2或x>2. 又有
可得x<-2或x>2. 又有 可得x<1.所以
可得x<1.所以
 .所以C选项不正确.由命题
.所以C选项不正确.由命题 的否定是
的否定是 使得
使得 .当x=3时成立.所以D正确.故选D.
.当x=3时成立.所以D正确.故选D.
考点:1.命题的否定.2.特称命题和全称命题.3.集合的概念4.充要条件.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知命题p:任意x R,都有x2+x+1>0,命题q:存在x
R,都有x2+x+1>0,命题q:存在x R,使得sinx+cosx=2,则下列命题中为真是真命题的是( )
R,使得sinx+cosx=2,则下列命题中为真是真命题的是( )
| A.p且q | B. p或q p或q | C.p或q | D. p且 p且 q q |
下列命题:①至少有一个x使x2+2x+1=0成立;②对任意的x都有x2+2x+1=0成立;
③对任意的x都有x2+2x+1=0不成立;④存在x使x2+2x+1=0成立.
其中是全称命题的有( )
| A.1个 | B.2个 | C.3个 | D.0个 |
“ 成立”是“
成立”是“ 成立”的( ).
成立”的( ).
| A.充分非必要条件. | B.必要非充分条件. |
| C.充要条件. | D.既非充分又非必要条件. |
已知直线 ⊥平面
⊥平面 ,直线m?平面
,直线m?平面 ,则“
,则“ ∥
∥ ”是“
”是“ ⊥m”的( )
⊥m”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分又不必要条件 |
下列说法中正确的是( )
A.若命题 为:对 为:对 有 有 ,则 ,则 使 使 ; ; |
B.若命题 为: 为: ,则 ,则 ; ; |
C.若 是 是 的充分不必要条件,则 的充分不必要条件,则 是 是 的必要不充分条件; 的必要不充分条件; |
D.方程 有唯一解的充要条件是: 有唯一解的充要条件是: |
下列有关命题的说法错误的是( )
A.命题“若 ”的逆否命题为:“若 ”的逆否命题为:“若 ” ” |
B.“x=1”是“ ”的充分不必要条件 ”的充分不必要条件 |
C.若 为假命题,则p、q均为假命题 为假命题,则p、q均为假命题 |
D.对于命题  ,则 ,则 |
 :若
:若 ,则
,则 ;命题
;命题 :已知非零向量
:已知非零向量 则“
则“ ”是“
”是“ ”的充要条件.则下列各命题中,假命题的是( )
”的充要条件.则下列各命题中,假命题的是( )



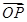 =x
=x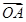 +y
+y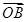 +z
+z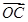 (x、y、z∈R),
(x、y、z∈R),