题目内容
已知抛物线C：y=x2+mx+2与经过A（0，1），B（2，3）两点的线段AB有公共点，则m的取值范围是（ ）A．（-∞，-1]∪[3，+∞）
B．[3，+∞）
C．（-∞，-1]
D．[-1，3]
【答案】分析：线段AB：y=x+1（0≤x≤2），与y=x2+mx+2联立得x2+（m-1）x+1=0，已知条件即此方程在[0，2]内有根，至此划归为根的分布问题．令f（x）=x2+（m-1）x+1 又f（0）=1＞0结合f（x）的图象求解．
解答：解：根据题意：线段AB：y=x+1（0≤x≤2），与y=x2+mx+2联立得：
x2+（m-1）x+1=0，
令f（x）=x2+（m-1）x+1 又f（0）=1＞0，
即函数在[0，2]上有交点，
∴
或f（2）＜0
解得：m≤-1
故选C
点评：本题主要考查直线与抛物线的位置关系，同时还考查了转化思想，数形结合思想，函数思想等．
解答：解：根据题意：线段AB：y=x+1（0≤x≤2），与y=x2+mx+2联立得：
x2+（m-1）x+1=0，
令f（x）=x2+（m-1）x+1 又f（0）=1＞0，
即函数在[0，2]上有交点，
∴
或f（2）＜0解得：m≤-1
故选C
点评：本题主要考查直线与抛物线的位置关系，同时还考查了转化思想，数形结合思想，函数思想等．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
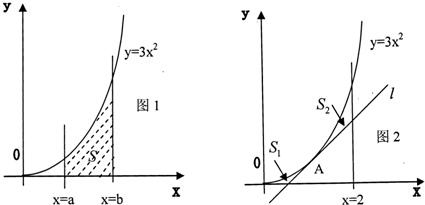
)2=r2(r＞0)有一个公共点，且在A处两曲线的切线为同一直线l.
)2=r2(r＞0)有一个公共点，且在A处两曲线的切线为同一直线l.