题目内容
如右图: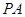 切
切 于点
于点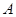 ,
,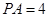 ,
,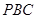 过圆心
过圆心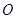 ,且与圆相交于
,且与圆相交于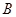 、
、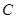 两点,
两点,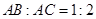 ,则
,则 的半径为 .
的半径为 .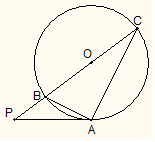
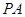 切
切 于点
于点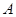 ,
,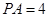 ,
,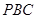 过圆心
过圆心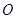 ,且与圆相交于
,且与圆相交于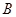 、
、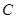 两点,
两点,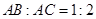 ,则
,则 的半径为 .
的半径为 .
3
此题答案为3
由题中条件:“PA切⊙O于点A”得弦切角与∠ACP相等得两三角形相似,得比例关系求出PC,最后利用切割线定理求出半径即可.
解:∵PA是切线,
∴∠BAP=∠ACP,
∵∠P=∠P,
∴△PAB~△PCA,则
即 ,
,
∴PC=8.设圆的半径为r,
由切割线定理PA2=PB?PC得,16=(8-2r)×8.
解出r=3.
故填:3.
由题中条件:“PA切⊙O于点A”得弦切角与∠ACP相等得两三角形相似,得比例关系求出PC,最后利用切割线定理求出半径即可.
解:∵PA是切线,
∴∠BAP=∠ACP,
∵∠P=∠P,
∴△PAB~△PCA,则

即
 ,
,∴PC=8.设圆的半径为r,
由切割线定理PA2=PB?PC得,16=(8-2r)×8.
解出r=3.
故填:3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 曲线
曲线 有4个不同的交点.
有4个不同的交点.
 是的
是的 的直径,
的直径, 、
、 、
、 是
是 ,
,
 ( ).
( ).



 与
与 切于点
切于点 ,
, ,
, ,则
,则




 为参数)的半径为 ,若圆C与直线
为参数)的半径为 ,若圆C与直线 相切,则
相切,则
 。
。