题目内容
3名志愿者在10月1日至10月5日期间参加社区服务工作,若每名志愿者在这5天中任选两天参加社区服务工作,且各名志愿者的选择互不影响.求(Ⅰ)这3名志愿者中在10月1日都参加社区服务工作的概率;
(Ⅱ)这3名志愿者中在10月1日至多有1人参加社区服务工作的概率.
分析:解法一:(I)根据每名志愿者在这5天中任选两天参加社区服务工作,则在10月1日都参加社区服务工作,则表示在其余四天只有一天参加社区服务工作,代入古典概型公式求出概率,
(II)在10月1日至多有1人参加社区服务工作包括两种情况,一是正好有一人,另外是一个人都没有,根据(I)的思路,结合互斥事件概率加法公式,可以求解.
解法二:(I)根据每一天补抽中的概率均为
,根据相互独立事件概率乘法公式,易得结果,
(II)在10月1日至多有1人参加社区服务工作包括两种情况,一是正好有一人,另外是一个人都没有,根据(I)的思路,结合互斥事件概率加法公式,可以求解.
(II)在10月1日至多有1人参加社区服务工作包括两种情况,一是正好有一人,另外是一个人都没有,根据(I)的思路,结合互斥事件概率加法公式,可以求解.
解法二:(I)根据每一天补抽中的概率均为
| 2 |
| 5 |
(II)在10月1日至多有1人参加社区服务工作包括两种情况,一是正好有一人,另外是一个人都没有,根据(I)的思路,结合互斥事件概率加法公式,可以求解.
解答:解法一:(I)这3名志愿者中在10月1号参加社区服务工作的人数恰好为3人的事件为A
P(A)=
=
这3名志愿者中在10月1号参加社区服务工作的人数恰好为3人的概率为
.
(Ⅱ)这3名志愿者中在10月1号参加社区服务工作的人数至多为1人的事件为B
P(B)=
+
=
+
=
这3名志愿者中在10月1号参加社区服务工作的人数至多为1人的概率为
.
解法二:
(I)这3名志愿者中在10月1号参加社区服务工作的人数恰好为3人的事件为A
P(A)=(
)3=
这3名志愿者中在10月1号参加社区服务工作的人数恰好为3人的概率为
.
(Ⅱ)这3名志愿者中在10月1号参加社区服务工作的人数至多为1人的事件为B
P(B)=(
)3+
(
)(
)2=
+
=
这3名志愿者中在10月1号参加社区服务工作的人数至多为1人的概率为
.
P(A)=
(
| ||
(
|
| 8 |
| 125 |
这3名志愿者中在10月1号参加社区服务工作的人数恰好为3人的概率为
| 8 |
| 125 |
(Ⅱ)这3名志愿者中在10月1号参加社区服务工作的人数至多为1人的事件为B
P(B)=
(
| ||
(
|
| ||||||
(
|
| 27 |
| 125 |
| 54 |
| 125 |
| 81 |
| 125 |
这3名志愿者中在10月1号参加社区服务工作的人数至多为1人的概率为
| 81 |
| 125 |
解法二:
(I)这3名志愿者中在10月1号参加社区服务工作的人数恰好为3人的事件为A
P(A)=(
| 2 |
| 5 |
| 8 |
| 125 |
这3名志愿者中在10月1号参加社区服务工作的人数恰好为3人的概率为
| 8 |
| 125 |
(Ⅱ)这3名志愿者中在10月1号参加社区服务工作的人数至多为1人的事件为B
P(B)=(
| 3 |
| 5 |
| C | 1 3 |
| 2 |
| 5 |
| 3 |
| 5 |
| 27 |
| 125 |
| 54 |
| 125 |
| 81 |
| 125 |
这3名志愿者中在10月1号参加社区服务工作的人数至多为1人的概率为
| 81 |
| 125 |
点评:本题考查的知识点是相互独立事件的概率乘法公式,及互斥事件概率加法公式,计算一个事件的概率,首先我们要分析这个事件是分类的(分几类)还是分步的(分几步),然后再利用加法原理和乘法原理进行求解.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
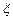 表示这3名志愿者在10月1号参加志愿者服务工作的人数,求随机变量
表示这3名志愿者在10月1号参加志愿者服务工作的人数,求随机变量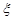 表示这3名志愿者在10月1号参加志愿者服务工作的人数,求随机变量
表示这3名志愿者在10月1号参加志愿者服务工作的人数,求随机变量