��Ŀ����
(��������12��)
��֪3��־Ը����10��1����10��5���ڼ�μ�2011������־Ը�������
��1����ÿ��־Ը����5������ѡһ��μ��������������Ҹ�־Ը�ߵ�ѡ��Ӱ�죬��3��־ԭ��ǡ������3��μ������������ĸ��ʣ�
��2����ÿ��־Ը������5������ѡ����μ��������������Ҹ�־Ը�ߵ�ѡ��Ӱ�죬��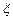 ��ʾ��3��־Ը����10��1�Ųμ�־Ը�߷����������������������
��ʾ��3��־Ը����10��1�Ųμ�־Ը�߷����������������������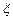 ����ѧ������
����ѧ������
�⣺��1��3��־Ը��ÿ����ѡһ��μ����������� �ֲ�ͬ�Ľ����
�ֲ�ͬ�Ľ����
��Щ������ֵĿ����Զ���ȣ�
�衰3��־Ը��ǡ������3��μ�������������Ϊ�¼�A��
����¼������� �ֲ�ͬ�Ľ��������
�ֲ�ͬ�Ľ��������
��3��־Ը��ǡ������3��μ������������ĸ���Ϊ ��������6��
��������6��
��II���ⷨ1���������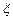 �Ŀ���ȡֵΪ0��1��2��3
�Ŀ���ȡֵΪ0��1��2��3  ��
��
 ��
�� ��������8��
��������8��
��������εķֲ���Ϊ��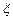
0 1 2 3 P 




��������12��
�ⷨ2��ÿ��־Ը����10��1�ղμ���������ĸ��ʾ�Ϊ
��������8��
������־Ը����10��1�ղμ��������������
 ��
�� ��������12��
��������12��
����

��ϰ��ϵ�д�
�����Ŀ