题目内容
在△ABC中，若asinA+bsinB＜csinC，则△ABC的形状是________．
钝角三角形
分析：利用正弦定理和余弦定理即可得出．
解答：由正弦定理可得
＞0，∴
，
，
．
∵asinA+bsinB＜csinC，∴
，即a2+b2＜c2．
∴
＜0．
∵0＜C＜π，∴
．
∴角C设钝角．
∴△ABC的形状是钝角三角形．
故答案为钝角三角形
点评：熟练掌握正弦定理和余弦定理是解题的关键．
分析：利用正弦定理和余弦定理即可得出．
解答：由正弦定理可得
＞0，∴，，．∵asinA+bsinB＜csinC，∴
，即a2+b2＜c2．∴
＜0．∵0＜C＜π，∴
．∴角C设钝角．
∴△ABC的形状是钝角三角形．
故答案为钝角三角形
点评：熟练掌握正弦定理和余弦定理是解题的关键．
练习册系列答案
相关题目
（1）如图，平行四边形ABCD中，M、N分别为DC、BC的中点，已知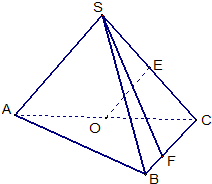
如图，在三棱锥S-ABC中，侧面SAC与底面ABC垂直，E，O分别是SC、AC的中点，SA=SC=
，BC=
AC，∠ASC=∠ACB=90°．
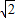，BC=
AC，∠ASC=∠ACB=90°．