题目内容
某电器商经过多年的经验发现本店每月出售的电冰箱的台数ξ是一个随机变量,它的分布列为P(ξ=k)=
解:设月初电器商购进的冰箱的台数为x,月收益为η元,则η是随机变量ξ的函数,且η=
![]()
因此,Eη=300x×![]() +[300-100(x-1)]×
+[300-100(x-1)]×![]() +[2×300-100(x-2)]×
+[2×300-100(x-2)]×![]() +…+[300(x-1)-100]×
+…+[300(x-1)-100]×![]() =300x(12-x+1)×
=300x(12-x+1)×![]() +
+![]() [300×
[300×![]() -100×
-100×![]() ]=
]=![]() ×(-2x2+38x).
×(-2x2+38x).
由于x为整数,所以当x=9或10(台)时,Eη最大,即电器商月初购进9台或10台电冰箱时,收益最大.
点评:依据题意可列出获利的平均数(即数学期望)的函数,求出其最值及达到最值的条件就可得解.

练习册系列答案
相关题目
某电器商经过多年的经验发现本店每个月售出的电冰箱的台数![]() 是一个随机变量,它的分布列如下:
是一个随机变量,它的分布列如下:
|
| 1 | 2 | 3 | …… | 12 |
| P |
|
|
| …… |
|
设每售出一台电冰箱,电器商获利300元。如销售不出而囤积于仓库,则每台每月需花保养费100元。问电器商每月初购进多少台电冰箱才能使自己月平均收益最大?
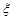 是一个随机变量,它的分布列为:
是一个随机变量,它的分布列为: ;设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元. 问电器商每月初购进多少台电冰箱才能使月平均收益最大?
;设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元. 问电器商每月初购进多少台电冰箱才能使月平均收益最大?