题目内容
必做题:解答时应写出文字说明、证明过程或演算步骤.已知函数f(x)=ln(ax+1)+
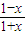 ,x≥0,其中a>0.
,x≥0,其中a>0.(1)若f(x)在x=1处取得极值,求a的值;
(2)若f(x)的最小值为1,求a的取值范围.
【答案】分析:(1)求导函数,根据f(x)在x=1处取得极值,可得f'(1)=0,即可求得a的值;
(2)求导函数,分类讨论:a≥2,则f'(x)>0恒成立,f(x)在[0,+∞)上递增,f(x)的最小值为f(0)=1;0<a<2,可得f(x)在x=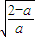 处取得最小值f(
处取得最小值f(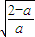 )<f(0)=1,由此可得a的取值范围.
)<f(0)=1,由此可得a的取值范围.
解答:解:(1)求导函数可得f′(x)= .
.
∵f(x)在x=1处取得极值,
∴f'(1)=0,∴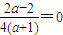 ,∴a=1;
,∴a=1;
(2)f′(x)=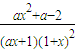 ,
,
∵x≥0,a>0,∴ax+1>0,1+x>0.
当a≥2时,在区间(0,+∞)上f′(x)≥0,f(x)递增,f(x)的最小值为f(0)=1.
当0<a<2时,由f′(x)>0,解得x>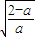 ;由f′(x)<0,解得x<
;由f′(x)<0,解得x<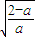 .
.
∴f(x)的单调减区间为(0,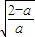 ),单调增区间为(
),单调增区间为(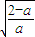 ,+∞).
,+∞).
于是,f(x)在x=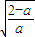 处取得最小值f(
处取得最小值f(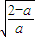 )<f(0)=1,不合.
)<f(0)=1,不合.
综上可知,若f(x)得最小值为1,则a的取值范围是[2,+∞) …10分
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的极值与最值,正确求导是关键.
(2)求导函数,分类讨论:a≥2,则f'(x)>0恒成立,f(x)在[0,+∞)上递增,f(x)的最小值为f(0)=1;0<a<2,可得f(x)在x=
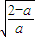 处取得最小值f(
处取得最小值f(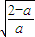 )<f(0)=1,由此可得a的取值范围.
)<f(0)=1,由此可得a的取值范围.解答:解:(1)求导函数可得f′(x)=
 .
.∵f(x)在x=1处取得极值,
∴f'(1)=0,∴
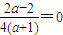 ,∴a=1;
,∴a=1;(2)f′(x)=
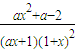 ,
,∵x≥0,a>0,∴ax+1>0,1+x>0.
当a≥2时,在区间(0,+∞)上f′(x)≥0,f(x)递增,f(x)的最小值为f(0)=1.
当0<a<2时,由f′(x)>0,解得x>
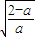 ;由f′(x)<0,解得x<
;由f′(x)<0,解得x<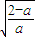 .
.∴f(x)的单调减区间为(0,
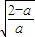 ),单调增区间为(
),单调增区间为(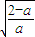 ,+∞).
,+∞).于是,f(x)在x=
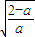 处取得最小值f(
处取得最小值f(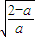 )<f(0)=1,不合.
)<f(0)=1,不合.综上可知,若f(x)得最小值为1,则a的取值范围是[2,+∞) …10分
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的极值与最值,正确求导是关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 ,x≥0,其中a>0.
,x≥0,其中a>0.