题目内容
（09年莱阳一中期末理）（14分)设向量
，函数
在[0，l]上的最小值与最大值的和为
，又数列
满足：
。
(1)求证：
；
(2)求
的表达式；
(3) 
试问数列
中，是否存在正整数k，使得对于任意的正整数n都有
成立？证明你的结论。
解析：（1）证明：
，因为对称轴
，所以在
上为增函数，∴
……………………………………4分
（2）解：由
得
两式相减得
，………………………………7分
当n=1时，
当
时，
即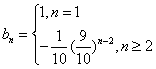
……………………………………………………9分
（3）解：由（1）与（2）得
，
所以当
时，
，
当
时，
，
当
时，
…………………………………………………………………………13分
所以存在正整数
，使得对于任意的正整数n，都有
成立……………………14分
练习册系列答案
相关题目
中，
为
中点，
为
中点，且△
为正三角形。
∥平面
；
平面
，
，求三棱锥
的体积。
，在其图象上一点
处的切线的斜率记为
．
在区间
上是单调递减函数，求
的最小值。
，
，
，
，
，
．
，其中向量
，
。
的最小正周期和在
上的单调递增区间；
时，
恒成立，求实数m的取值范围．