Question

（2013•湛江二模）在圆（x-2）²+（y-2）²=4内任取一点，则该点恰好在区域

x+2y-5≥0 x-2y+3≥0 x≤3

内的概率为

1

2π

．

Answer 1

分析：作出题中不等式组表示的平面区域，得如图的△ABC及其内部，由此结合几何概型计算公式和面积公式，即可算出所求的概率．

解答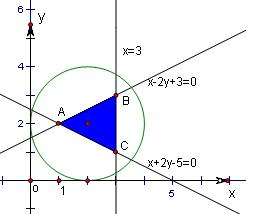：解：作出不等式组

x+2y-5≥0 x-2y+3≥0 x≤3

表示的平面区域，
得到如图的△ABC及其内部，其中A（1，2），B（3，3），C（3，1）
∵△ABC位于圆（x-2）²+（y-2）²=4内的部分，
∴在圆（x-2）²+（y-2）²=4内任取一点，则该点恰好在区域

x+2y-5≥0 x-2y+3≥0 x≤3

内的概率为P=

S△ABC

S圆

=

1 2 ×2×2

22×π

=

1

2π

．
故答案为：

1

2π

．

点评：本题给出圆（x-2）²+（y-2）²=4内任取一点，求该点恰好在区域内的概率．着重考查了二元一次不等式组表示的平面区域和几何概型等知识，属于基础题．